Posted by Nodus Labs | March 21, 2021
Fractal Variability Feedback System

The human body has a fractal essence: not only on the level of the physical structure but also in terms of the dynamics of many processes that happen within. The brain activity [1], healthy heartbeat [2], breathing [3], speech [4], and physical movement [5, 6] exhibit fractal dynamics or variability. The systems that exhibit fractal dynamics are known to be more resilient and adaptive. Therefore, it is possible that if we can modulate fractality in a system, we can support its homeostasis, make it more resilient and adaptive.
In the context of the EightOS project that took place during the Gwangju Biennale 2021, we decided to explore how to modulate fractality within individuals and a group as well as the implications of this approach.
What is the Fractal Time Series?
Fractals are often associated with the beautiful Mandelbrot shapes where self-affinity is present across multiple scales.

Fractals are very much present in nature because they are very efficient for constructing complex multifunctional patterns based on a set of a few simple principles. Like a concise evolutionary program that can carry itself out in time and space.

A fractal process will also exhibit self-similarity across different scales: no matter how close or how far we look. This is also why fractal phenomena are also called scale-free: they exhibit a similar kind of dynamics across the scales.
When we are talking about time and fractals we mainly talk about variability. This variability may be present between the onset of events (e.g. the heartbeat or breathing) or within the dynamical process itself (e.g. movement velocity or neuronal activity).
Processes that are fractal in nature will also have 1/f “pink noise” dynamics [7, 8]. The higher is the frequency (f), the lower is the amplitude. The lower is the frequency (rare events), the higher is the amplitude. This means that there are multiple small oscillations and a few, but a significant number of the big ones (in other words, there’s a power-law relation between the frequency and the amplitude).
If we are referring to a dynamic process such as the natural movement of the body (or its acceleration), there will be many small fluctuations and a few big ones. If we are referring to the variability between the events, such as the heartbeats, this means the most of the time the deviations of the distances between the heartbeats will differ by not much but occasionally there will be longer or shorter distances and there will be a relatively significant number of them. The distribution of those deviations will not follow a uniform bell-curve (around a certain average), but, rather, the power law.
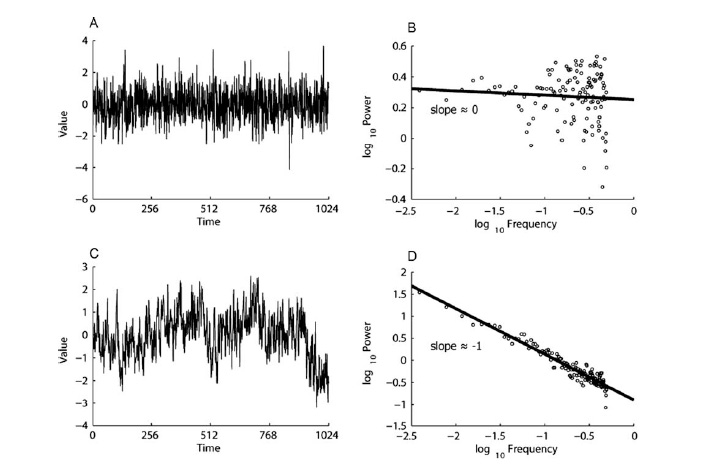
C – pink noise, the deviations follow the power law.
Interestingly, fractal dynamics is also present in human cognition [9, 10] and emotional shifts [11, 12], which may be an indication of the metastable nature of human cognition and perception. Specifically, Rabinovitch and Bystritsky [10] have shown that winnerless competition may be one of the underlying principles of human attention, which also enables its multitasking properties and the ability to adapt to the rapidly changing environment. That means multiple processes are interacting and competing for resources (energy), but none overtakes the others.
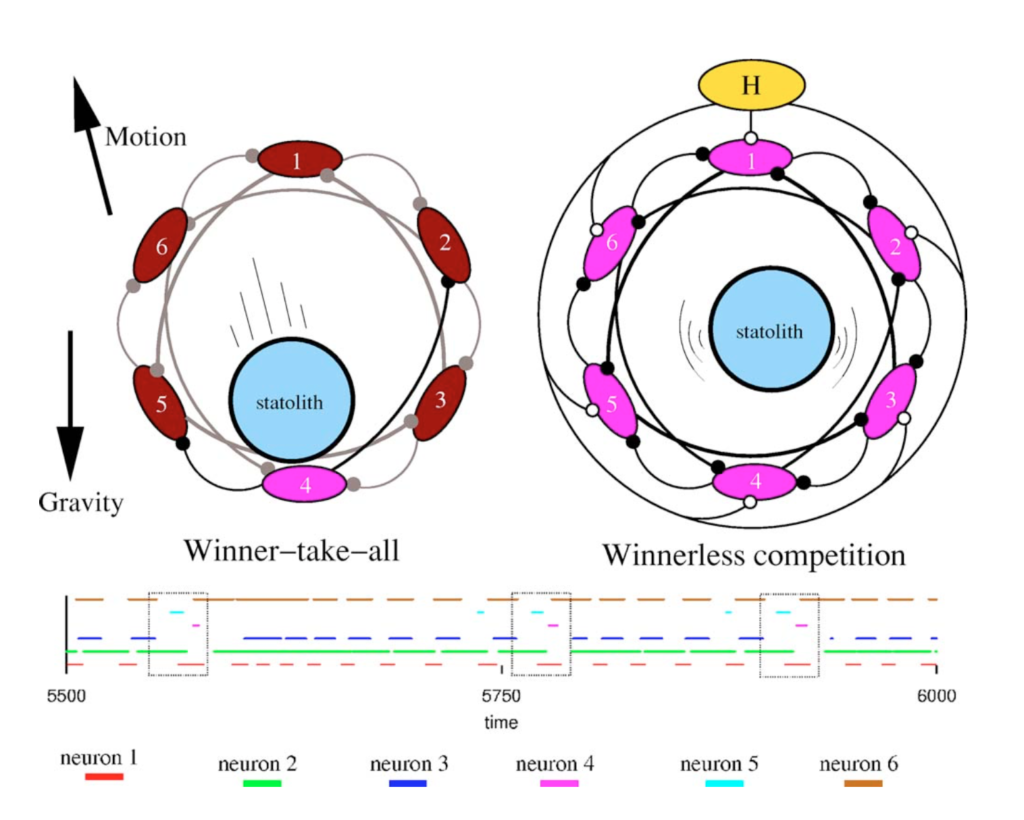
A similar conclusion was also reached by Katerndahl et al [12] who showed that healthy dynamics of mood variation may be characterized by a circadian pattern with underlying chaos. For those who are in depression, the circadian pattern of mood variation may be lost, while in panic disorder, the underlying chaos may be lost. Therefore, pathologies lack fractality and this may be due to the fact the system becomes less resilient and adaptive to external change.
This is confirmed by the multiple studies that suggest that the existence of fractal phenomena signifies the
- presence of memory in a system [7, 8]
- several underlying interacting processes which co-exist in the state of “winnerless competition” (i.e., breathing, heartbeat, walking), where none overtakes the others.
- adaptive behavior influenced by external factors and instabilities [8]
How to Be and to Think in a Fractal Way?
We have shown above that fractal phenomena are present in many natural processes, including human movement, but also in cognition and emotional responses to the environment. If their presence makes a system more adaptive and resilient, can we modulate fractality on the level of human behavior? What would it be like to move and to think in a fractal way?
In the context of the EightOS project during Gwangju Biennale, we needed to conceive of a feedback mechanism that would provide us with real-time data about the fractality of our activity. This could be done using wearable sensors and fitness trackers, which could then be sending the data about the movement and attention on a certain task to a program, which would estimate the fractality of that movement.

In the context of our project, we used xSens Dot motion sensors to track movement acceleration. The data was sent to the computer via the EightOS Fractal Control software (based on xSens server), which was modified by us to convert the sum of the movement acceleration across 3 axes (for every sensor and for all the sensors at once) into a stream of data, which was then sent to a python-based detrended fluctuation analysis (DFA) algorithm [13].

DFA is often used to measure the fractality of heart rate variability and is a quick way to calculate the alpha exponent of time series (which shows the relation between the log of the scale and the log of the frequency — read more about how DFA works in the Appendix below). The resulting alpha-exponent number (usually from 0.3 to 1.4) will indicate the current state of the movement. When the alpha exponent is between 0.85 and 1.15 the movement is fractal (1 for the perfect fractal dimension). We then feed this data to the part of the program that projects the resulting alpha-exponent and the associated symbol (one for each of the 4 possible states) back to the movers. Additionally, the sonic and haptic feedback are sent via the EightOS tripod sensors.


The visual, sonic, and haptic feedback is then used by the movers to adjust the dynamics.
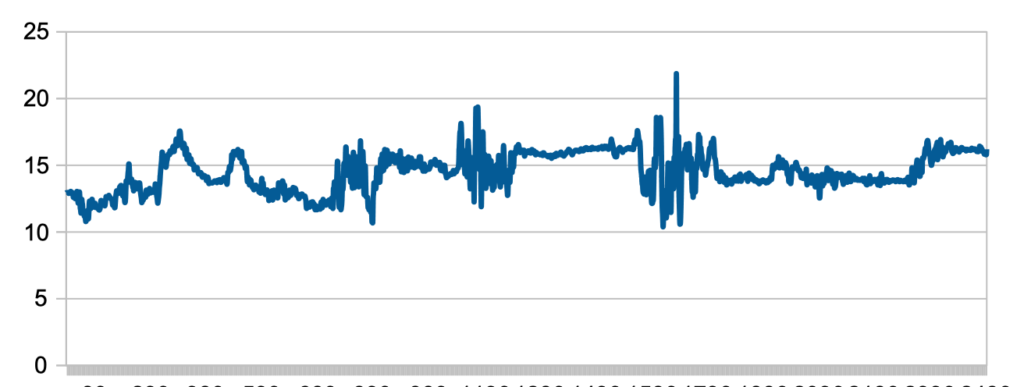
If the goal is to be in a fractal (adaptive, variable) state, they will be steering their movement towards the corresponding dynamics. For instance, if they get the feedback that their movement is too repetitive (alpha exponent around 0.4 – 0.6), then will introduce more variability into the movement. If they get the feedback that their movement dynamics is too complex (alpha > 1.3), they will simplify it. In general, fractality is achieved when the movement consists of many small changes (in velocity, direction) and a few, but a significant number of the occasional deviations (faster speed movement, sudden change of direction, etc). This is how it looks like as a result (from one of the experiments):
If we look at the corresponding graph that shows acceleration across the different axes for one of the sensor, it looks something like this:
Another approach was based on shifting between the different states (introducing chaotic variability in the phase shifts between the different alpha exponents). The objective, in this case, would be not to stay in one state, but to switch between them: a repetitive state would morph into a regular movement, which would then shift into fractal, and into complex, only to turn back to the repetitive mode.
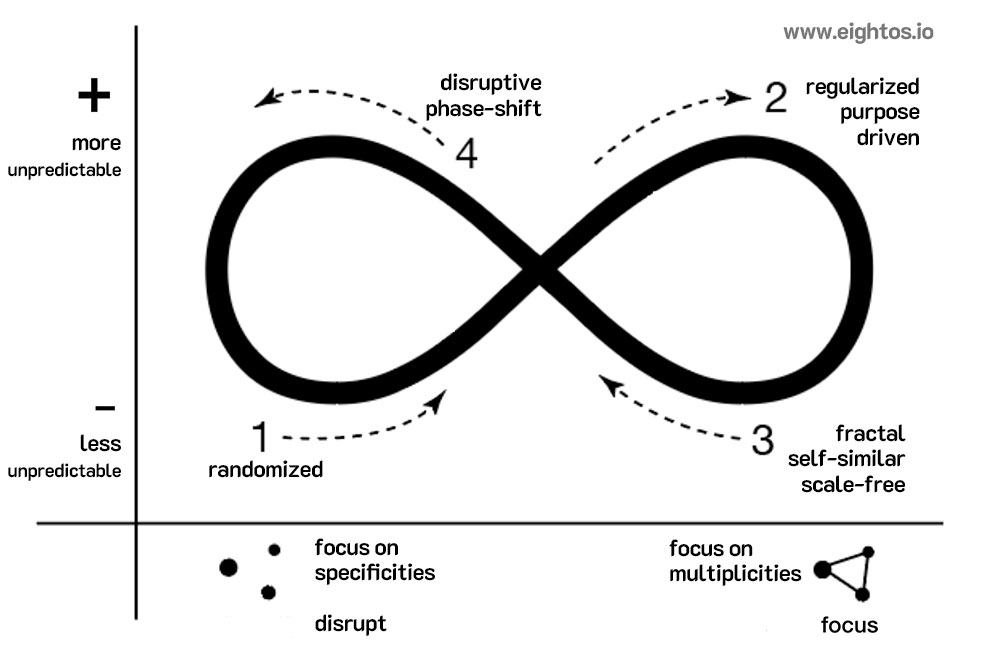
After applying this feedback in the experimental setting, the movements of every individual, as well as the dynamics of the whole group, appeared to be more versatile and diverse. If there was an unexpected event, it was easier for the movers to deal with it, while the choreography itself became less predictable and had more variability in terms of the dynamics and content. You can read more about the movers’ experience in the EightOS report about Gwangju Biennale working process.
Next Step: Fractal Cognition
The project in Gwangju has given us the possibility to experiment with fractality in the context of physical movement. We could also observe the effects that it has on perception as well — it seemed that the attention shifts followed a similar kind of dynamics: multiple small oscillations as well as a few, but a significant number of bigger ones.
We have already attempted to apply a similar approach in our study of cognitive dynamics. In our previous article on variability of attention we proposed an approach that makes use of network science to create cognitive structures that stimulate variability. There is a well-known link between scale-free networks and fractality, mainly coming from neuroscience, where the structure of the network affects the dynamics that emerges within. In a similar way, we propose that a text, or a narrative network structure, could also be organized in such a way that every time our attention comes into contact with it, it would follow a chaotically intermittent pattern: reading (or writing, or thinking) in a way that connects the related concepts together (within the same cluster) with a few, but a significant number of occasional jumps to completely different topics that are only distantly related. If a narrative is created this way, or, alternatively, if we read through a narrative in this way, we can make the perception of content fractal in its dynamic nature.
The advantage of this approach is that we stay open and adaptive in our perspective. We have the ability to focus on a specific cluster of ideas and yet have an overview of a bigger picture.
Another approach is to stimulate the shifts of attention using a timer, in a similar way the movement shifts are stimulated by the visual feedback provided to the dancers in the example above. This timer would provide the feedback to shift attention or to make a break. But instead of doing it, as most timers do, in a regular fashion, the timer would ensure that there is chaotic variability between the periods of activity and rest, making it more “natural” in a fractal way. This is the direction that we are going to develop the EightOS fractal control system, so it can operate both on the level of the movement and on the level of attention (and state changes).
Appendix: Detrended Fluctuation Analysis
It may be interesting to look closer at how the Detrended Fluctuation Analysis approach [13] works as it sheds more light on the phenomenon of fractality.
The DFA algorithm does the following:
– take a discrete time-series data
– detrend it and normalize it (so the values are positive and the trends are removed) — we only have fluctuations left
– calculate the sum of the square of the deviations for the different time scales: the short ones (e.g. fraction of a second) and the long ones (e.g. several seconds)
– build the log / log graph where on the X axis we have the size of the scale, on the Y axis we have the sums of the fluctuations
– plot the values obtained and calculate the slope of the line — this will be the alpha exponent.
In simple terms, Alpha exponent shows how much the accumulation of fluctuations in movement increases as we increase the time period we look at. If the increase in the fluctuations as we increase the time scale, the Alpha exponent is zero, meaning that they will always revert to the mean. If we increase the scale 4 times but the number of fluctuations only increases 2 times, then alpha-exponent is 0.5 and we have a random process. In a random process the fluctuations accumulate, but the absence of occasional high-amplitude oscillations reduces the alpha component. Now, if we bring in an occasional high-amplitude fluctuation, we will move towards a positively correlated process: the more we move, the more fluctuations we accumulate. When the number of those high-frequency oscillations is high enough, in fact, exactly at the right “sweet-spot,” we will reach fractality. This means that no matter what scale we look at, the pattern of fluctuation will be the same (so it’s self-similar across different scales or “scale-free”). Introduce more change, and we look at a situation where big time scales will yield a very high number of changes, so the movement becomes fractal (it is not similar across the scales anymore).
References
[1] Werner, G (2009). Fractals in the Nervous System: conceptual implications for Theoretical Neuroscience. (arxiv)
[2] Stiedel, O; Meyer, M (2003). Self-affine fractal variability of human heartbeat interval dynamics in health and disease. Eur J Appl Physiol, 90, 305–316. https://doi.org/10.1007/s00421-003-0915-2
[3] Hughson R.L., Yamamoto Y., Fortrat JO. (1995) Is the Pattern of Breathing at Rest Chaotic?. In: Semple S.J.G., Adams L., Whipp B.J. (eds) Modeling and Control of Ventilation. Advances in Experimental Medicine and Biology, vol 393. Springer, Boston, MA. https://doi.org/10.1007/978-1-4615-1933-1_3
[4] T Kello, G, Anderson, G, Holden, J, Van Orden, G. (2008) The Pervasiveness of 1/f Scaling in Speech Reflects the Metastable Basis of Cognition. Cognitive Sciences. 32:1217-1231
[5] Yamada, N. (1995). Chaotic swaying of the upright posture. Human movement science.
[6] D’Mello, S., Dale, R., & Graesser, A. (2011). Disequilibrium in the mind, disharmony in the body. Cognition & Emotion, 00(00), 1–13.
[7] Rickles D , Hawe P, Shiell A. (2007) A simple guide to chaos and complexity. Journal of Epidemilogoy & Community Health. 61:933–937.
[8] Bak, P., Tang, C., & Wiesenfeld, K. (1987). Self-organized criticality: An explanation of the 1/ f noise. Physical Review Letters, 59(4), 381–384.
[9] Bystritsky, a, Nierenberg, a a, Feusner, J. D., & Rabinovich, M. (2012). Computational non-linear dynamical psychiatry: A new methodological paradigm for diagnosis and course of illness. Journal of Psychiatric Research, 46(4), 428–435.
[10] Rabinovich MI, Huerta R, Varona P, Afraimovich VS (2008) Transient Cognitive Dynamics, Metastability, and Decision Making. PLOS Computational Biology 4(5): e1000072. https://doi.org/10.1371/journal.pcbi.1000072
[11] Rabinovich, M. I., & Muezzinoglu, M. K. (2010). Nonlinear dynamics of the brain: emotion and cognition. PhysicsUspekhi, 53(4), 357-372. doi:10.3367/UFNe.0180.201004b.0371
[12] Katerndahl, D., Ferrer, R., Best, R., & Wang, C.-P. (2007). Dynamic patterns in mood among newly diagnosed patients with major depressive episode or panic disorder and normal controls. Primary care companion to the Journal of clinical psychiatry, 9(3), 183–7
[13] Hardstone, R., Poil, S.-S., Schiavone, G., Jansen, R., Nikulin, V., Mansvelder, H., & Linkenkaer-Hansen, K. (2012). Detrended Fluctuation Analysis: A Scale-Free View on Neuronal Oscillations. Frontiers in Physiology, 3, 450. https://doi.org/10.3389/fphys.2012.00450