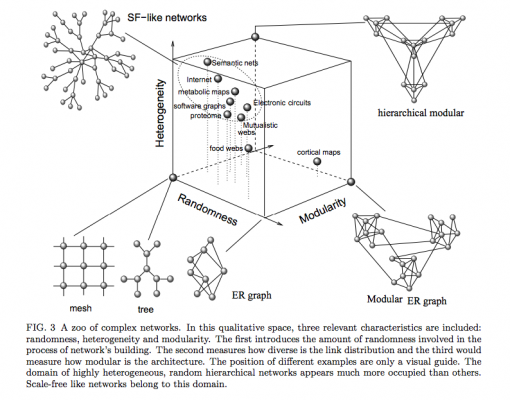
Information Theory of Complex Networks: on evolution and architectural constraints paper by Sole and Valverde (2004) features a very interesting chart that shows how different types of networks relate to each other in terms of their randomness, heterogeneity, and modularity. We’ve tried playing around with these different structures using InfraNodus network visualization tool to see how different types of networks have different structural properties.

Various types of Networks, Reproduced from Sole and Valverde (2004).

One extreme of the graph are regular lattices (meshes) and trees. These are usually man-made networks that have the lowest heterogeneity (e.g. the number of connections each node has is more or less the same) and lowest randomness (the probability of any two randomly chosen nodes to be wired to each other is very low or zero). Regular graphs tend to have long average paths and high clustering (as the nodes tend to be densely connected in groups). One real-life example of that is the graph of the relations between the organs and their relations to various emotions, ailments and elements — a man-made conceptual knowledge network. Another example are the hierarchical power structures present in the army.

Another extreme are the random ER (Erdos-Renyi) graphs, which are generated by starting with a disconnected set of nodes that are then paired with a uniform probability. Such random networks will have low heterogeneity (most nodes have the same number of connections), the degree distribution will be a Gaussian bell-shaped curve. Random graphs built after ER algorithm have short average paths and low clustering.

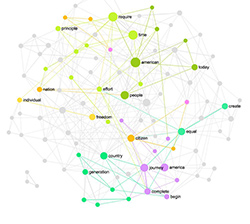
Most real-world networks, however, especially social networks, do not have homogeneous distribution of degree that regular or random networks have. The number of connections each node has in most networks varies greatly and they are positioned somewhere between regular and random networks. In fact, Watts and Strogatz (1998) proposed a model where the connections between the nodes in a regular graph were rewired with a certain probability. The resulting graphs were between the regular and random in their structure and are referred to as small-world (SW) networks. SW networks are very close structurally to many social networks in that they have a higher clustering and almost the same average path than the random networks with the same number of nodes and edges. SW networks usually have high modularity (groups of the nodes that are more densely connected together than to the rest of the network). The graph above shows a different type of a SW network though, the one that’s generated by rewiring the connections from within the interconnected modules to between these modules – an architecture that is often found in cortical maps (neural networks in the brain).

Finally, there’s a large class of so-called scale-free (SF) networks characterized by a highly heterogeneous degree distribution, which follows a “power-law” (Barabasi & Albert 1999). They are called scale-free, because zooming in on any part of the distribution doesn’t change its shape: there is a few, but significant number of nodes with a lot of connections and there’s a trailing tail of nodes with a very few connections at each level of magnification. Such networks are typical for the structure of the world wide web, semantic maps, electronic circuits. These structure combine heterogeneity and randomness, they can have low or high modularity and many SW networks are also scale-free.

…

If you are interested to explore more about various types of networks, try out our InfraNodus tool. You can build your own graphs in it using text-to-graph input, visualize all kinds of graphs and get statistical data on both the individual nodes and the whole network.