Posted by Nodus Labs | February 17, 2012
Information Epidemics and Synchronized Viral Social Contagion
By Dmitry Paranyushkin, Nodus Labs, Published February 2012 (PDF)
Abstract:
In this research we look into the network structures that are the most conducive for informational epidemics and synchronized viral contagion in the context of social networks. Specifically we are interested in the structures that enable informational cascades (simultaneous contagion of multiple nodes) as well as a sustained endemic level of epidemics within the communities. We find that the most efficient communication strategy entails increasing the connectivity of the network, randomizing its structure, and addressing the most densely connected groups first, ensuring that the message is propagated further using the supra-network between these groups and the lynchpins that connect different communities together. We also look into the necessary properties of a message for it to go viral. We show how our findings can be practically applied in the context of social network promotion and organizing live events. We also demonstrate how this knowledge can be used by communities to immunize themselves against unwanted ideological communication while still maintaining a degree of openness that allows them to remain innovative.
Workshop / Lecture Slideshow
View the slideshow on SlideShare
Presentation at re:publica 2012
PDF of the Paper
1. Introduction
Every community can be modeled as a network (Fig 1). The nodes are the people and the connections are interactions between them (Newman et al 2006). A vast range of methods and tools from network analysis can then be used to get more insight into the processes such as rumor propagation, information diffusion, trends, and collective action. 
Figure 1: Network visualization by Gephi (Bastian et al 2009)
In this research we are particularly interested to see how large groups of people can drastically change their opinion, adopt a new trend, come out to protest on the streets, adopt a certain ideology, have a memorable collective experience, or start using a certain product on mass scale. While all these social phenomena are diverse, one thing in common is that they involve information contagion that happens in a synchronized way, evoking a certain response from large groups of population at once.
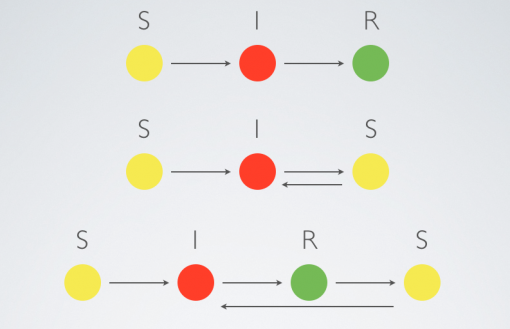
In network science the processes of information contagion can be studied using epidemic models. If we consider information as a disease, three different models can be used to model its proliferation through the network: SIS, SIRS and SIR (Ball 1997; Newman 2002). In the first model an element of the population (a node in a network) can be either susceptible (S) or infected (I) and goes through these stage one after the other: susceptible – infected – susceptible. According to the second model, the node also has a refractory stage (R) before it becomes susceptible again, so the states are: susceptible – infected – refractory – susceptible. Finally, in the third model once the node is infected once it cannot be infected again, so for each node the sequence is: susceptible – infected – removed (R). Depending on the nature of information studied, a certain model can be more suitable than another (Fig 2). 
Figure 2: Epidemic models SIR, SIS and SIRS
Using these models can shed some light on the dynamics of informational contagion when the transmitted message is modeled as a virus. Specifically, given that the message has self-replicating capabilities and that the structure of the network is known, it is possible to see whether the message will spread over the whole network or stay localized within a certain cluster or subgroup (Zhou et al 2007; Lambiotte & Panzarasa 2009; Ball 1997; Ball et al 2010). It is also possible to see whether contagion will occur in a synchronized way as an informational cascade or just sift gradually through the network (Kuperman & Abramson 2001; Lerman & Ghosh 2010; Xu et al 2008; Dodds & Watts 2005; Watts 2002).
In this research we are bringing together the research from network science, epidemiology, and viral marketing. Our interest is to find the necessary conditions for informational epidemics to spread over the whole network while maintaining endemic viral contagion levels at certain areas of the network. These areas of viral contagion would then periodically generate informational cascades (simultaneous contagion of many nodes) through the network in order to maintain epidemic levels above a certain level with the minimum outside intervention.
Such network would be autopoietic (Varela et al 1974) in that it self-replicates its own structure through informational contagion each time the virus-message is proliferated. It functions on the basis of polysingularity (Gabdulkhaev 2005), maintaining several centers of endemic contagion with occasional network-wide outbreaks. The dynamics of these outbreaks is a subject for another research, we can only speculate that their occurrence follows a chaotic pattern and that these centers of endemic contagion may be modeled as strange attractors in the complex structure of the network (Strogatz 1994; Mandelbrot 1999). In this research, however, we will focus on the structural properties of the network that enable these viral outbreaks to happen in the first place, as well as on the quality of the individual connections between the nodes that are more conducive to the network-wide contagion.
We also present two examples how the strategies we proposed could be applied into practice: one is a Facebook community and another one is a live entertainment event. In both cases we test if the strategies can be used to create more vibrant and active communities as compared to the control situations where none of the strategies have been implemented.
We believe that this research may be useful for a wide range of applications: from viral marketing and promotion to the study of ideologies, protest, and collective action. We also believe that the network structure we found to be the most conducive for informational contagion and viral outbreaks has as much potential to create benefit for its members as to be abused. Therefore it is also our goal to show how a network could maintain the capability for a collective action while being immunized against harmful ideologies.
2. Group Structure and Contagion
Information cascades (Bikhchandani et al 1993; Watts, 2002) describe a herd-like behavior exhibited by populations, where individuals are making decisions or take action based on external influence from the other individuals they are connected to. In other words, it’s a synchronized response to a certain incoming information. Such behavior can be modeled using epidemic models, where information cascade is a simultaneous transition of a group of nodes from susceptible (S) into infected (I) stage (Keeling 1999). During this stage they can infect the other susceptible nodes. After a period of time the nodes transition to the refractory (R) stage, which can be modeled using percolation graph (Callaway 2000). Depending on the nature of epidemic, the nodes in the refractory state can return to susceptible state again after a period of time. If this process happens simultaneously for a large number of nodes, the network will exhibit periodic behavior (Kuperman & Abramson 2001).
While there are many possible ways for information to spread through the network, this paper will focus on the global cascades (i.e. overtaking the majority of nodes) that can be triggered by exogenous events that involve a relatively small initial set of nodes relative to the system’s overall size.
In viral marketing this would account to finding a strategy of ensuring a message has the widest and the fastest possible reach with the least initial number of nodes carrying the message initially.
In terms of epidemics and network science this would account to finding which structures and communication patterns lead to the widest possible spread of disease in the shortest period of time.
We are also interested in the factors that make such activity periodic and increase the amplitude of each cascade. A higher amplitude means more capacity for a collective action, as nodes find themselves in a highly mobilized surrounding and therefore the threshold for adopting a trend or joining in the collective action decreases (Bikhchandani et al 1993).
It has been shown that the structure of the network is one of the defining factors for epidemic propagation. Rapid spread of a disease within tightly interconnected communities (such as families or workplaces) can lead to an epidemic outbreak in the whole network even if the connections between these communities are loose (Ball, 1997). This happens because the whole network can be seen as a supra-network of communities, in which individuals mix uniformly within the communities, and in addition, uniformly at a much lower rate within the population at large. Therefore, the communities tend to form a supra-network with short path lengths and the disease spreads much faster across the whole population over this supra-network once each individual community is fully infected (Ball, 1997; Newman et al 2006). It’s a very typical structural property of real life networks that are also referred to as small-world networks – highly clustered networks with short path lengths (Watts & Strogatz, 1998). Many small world networks have scale-free degree distribution following a power law (Barabasi & Albert, 1999), where a few, but significant number of nodes accumulate the most connections, while the majority of nodes have only a few. It has been shown (Kuperman & Abramson 2001) that such networks also do not have an epidemic threshold meaning that the disease can spread even if only a few selectively targeted most connected nodes are infected initially.
Therefore, the optimal information contagion strategy would be to target several tightly-knit groups at first, make sure that they are “infected” with information, and then let them spread that information further across the community supra-network to the rest of the groups (Fig 3).
An example of a successful use of this strategy is the virulent spread of Facebook network. Started at the Harvard university campus, it was first opened up to a few selected Ivy League institutions, moving on to quickly expand across other educational institutions across the US, finally opening up for everyone to register even if they don’t belong to an educational institution (Phillips, 2007).

Figure 3: Communities in a network spread infection across
the supra-network between one another.
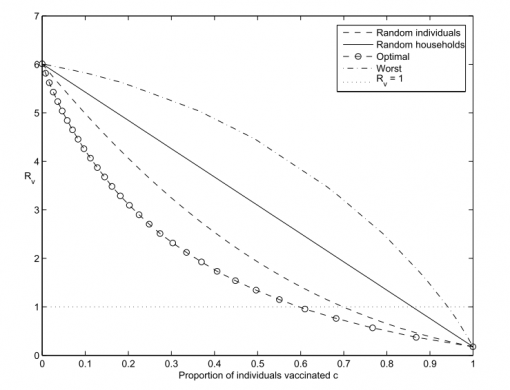
In this context it’s also interesting to mention the optimal immunization strategy. It has been shown that immunizing random households is less effective than immunizing random individuals, which is still less effective than immunizing a certain proportion of each household, so that the total number of infected members is equalized across the network (Ball 1997; Ball et al 2010). This is also referred to as equalization strategy, which was found to be the optimal one (see Fig 4).

Its efficiency has been recently confirmed in a study including UK households, where three immunization strategies were compared: random immunization, household immunization and children immunization. The latter strategy that effectively leaves an equal number of susceptibles in each household (i.e. the parents) was shown to be the most effective one that would reduce the spread of infection considerably in comparison to the other two strategies (House & Keeling, 2009).
If we now consider immunization as a certain resistance to information contagion (which often exists anyway), those networks where distribution of resistance across the nodes reflects the least effective immunization strategy would be more conducive to propagate information through the whole network. Therefore, before seeding the message it’s important to identify the structure of belief immunization across the network. If there is a choice, the networks where there are several groups that would be willing to accept the message in their entirety would be much more conducive to information contagion, than the networks where a certain percentage of population at large is willing to accept that message, even if the fraction of susceptible individuals is the same. In other words, antagonism is very conducive for information contagion as long as that information clearly belongs to one of the opposing sides. That means that there should be something within the message that entices the groups in their entirety to pass it on further across the network. We will discuss further what the properties of such message could be, but the important aspect that we want to emphasize here is the ability of such message to be interesting for a group (or to form a group) and for it to be compelling enough for the group members to propagate it further to each other and outside of the group.
An earlier example of Facebook is an instance of practical realization of this strategy (Phillips, 2007). When the social network was just started, a certain subgroup of the population was identified as the least immunized against the “contagion”, that is, the college students who already have tightly-knit communities and are prone to sharing information and looking up the information on their classmates. These groups were conducive to the initial proposition of Facebook to look at each other’s profiles privately. Then, once the initial seeding succeeded and all the educational institutions in the US were on Facebook, it opened up to the rest of the world at first bringing in students across the world (another example of segmentation), and only then enrolling the rest of the population.
Alternatively, before seeding the message the social structure could be rearranged in a such a way that there are tightly-knit groups forming that would be ready to accept a certain message as it does not contradict their belief system and those who are “immunized” could be excluded and form their own communities. This is a case of assortative mixing (grouping of nodes by interests), which has been shown to be typical for real-life social networks and it has also been demonstrated that such networks percolate more easily than their disassortative counterparts (Newman, 2002b), meaning that they are much more susceptible to information contagion.
This fact seems to be well-known to the most successful internet companies, which reconfigure communities to be determined by shared interests and belief, rather than demographic or geographic factors, creating so-called filter bubbles (Pariser 2011). Such filter bubbles produce consent within groups and foster assortative mixing by interest through recommendation algorithms. The resulting network can still be immunized against a certain belief, but in a much less efficient way, as we’ve shown above. Therefore, once the potential advertiser can target their message effectively to reach the groups by interests highly susceptible to the particular message they need to communicate, the efficiency of such campaign will benefit from epidemic spread of information that will follow.
Another example are the political and social campaigns that create antagonism within population (democrats vs. republications, gay vs. homophobic, left vs. right, hipster vs. the rest etc.) The resulting tightly-knit groups that may be disconnected from each other, but share the same interests become more prone to rapid information contagion throughout the whole subnetwork of interests. Moreover, it has been shown (Marvel et al. 2011) that when there is a certain antagonism in a network, the part of it that has more connections (edges between the nodes), will eventually take over the less densely connected part (of course, if that other part is at all prone to belief change). This has important consequences for political campaigners who base their campaigns on antagonism. When the opposing force reorganizes itself in opposition to the collective action of the minority, they may eventually take over as a result of the antagonistic policy assumed by the minority. Therefore, a more efficient agenda would be not the one based on antagonism to the prevailing model, but the one that takes into account the interests of majority and proposes a certain improvement in a non-antagonistic way (so that the opposing force cannot be formed simply on the basis of being against the minority).
If a group or an individual do not want to belong to such tightly-knit interest-based structure prone to information contagion, it is important that they open up their social circle to include the individuals that do not know each other, therefore expanding the diversity of communities they belong to and having access to contradicting information. Thus, introducing a certain dynamics that fosters randomness and openness into the group’s structure (Paranyushkin, 2011a) can effectively render the individuals within the group more immune to informational epidemics.
Practically, this is the differences between the political strategies utilized by Vladimir Putin and the main opposition protagonist in Russia Alexander Navalny (Ioffe, 2011). In response to declining ratings of the United Russia party Putin formed People’s Front, which had improvement of the current conditions as its main agenda without contradicting the prevailing majority. In the meanwhile Navalny acts as opposition, fighting against the prevailing majority represented by the United Russia party, which of course fights back by forming tightly-knit antagonistic groups, thus increasing its own efficiency for collective action as has been shown above. In addition, a slight worsening of its position may in fact provoke a more extreme retaliating action and thus increase the threshold for a collective action within the antagonistic group (Schelling 1960).
In such situation a much more effective strategy for Navalny would be to act as a sort of Trojan horse: gathering like-minded individuals around the concrete projects that offer improvement (such as RosPil.Info, which uncovers the cases of government corruption), while avoiding antagonistic relation to the prevailing majority. Once the number of individuals, the density and the strength of their connections equals the one of United Russia, a new ideological message could be seeded that would create antagonism within the network against United Russia party. This way the opposition would have much more chances to win, as by the time the call for action emerges it has a much larger base built over a period of time around the positive rather than antagonistic attitudes and therefore giving more chances for the political change to happen.
In this regard a recently published research on information propagation in networks has shown that the prevailing majority opinion in a population can be reversed by a small fraction of randomly distributed agents who consistently proliferate the opposing opinion (Xie et al 2011). It has been shown that once the number of the nodes committed to the message that opposes the majority reaches about 10% of the total network population, the time it takes for the entire population to adopt the opposing opinion dramatically decreases. This once again emphasizes the importance of building a loyal group following first, before spreading the message across the whole network.
To summarize, information contagion is the most efficient in small world networks when the initial seeding occurs within several groups that have the lowest immunization rate (opposing beliefs) against the information. Once information spreads across these groups, they will themselves spread it across the rest of the community using a supra-network of intra-group connections.
To fine-tune this strategy, one can also do some work prior to seeding. One approach is to select the part of the network that has the structure most prone to information contagion (several groups, which have the lowest threshold for the particular information that needs to be disseminated). Another approach is to rearrange the network in such a way that the members form two types of groups according to their being prone to the forthcoming message or susceptible to it. Once this process of network reorganization is done and the group constellations are stable for a period of time, the message can be seeded to the groups of susceptible individuals to ensure its fast dissemination across the network.
For groups or individuals to resist information contagion they should ensure there is always a certain dynamic contradiction within their groups, so that they are not completely homogeneous in their connectivity and beliefs.
3. Information Cascades
As we have been discussing contagion, it’s important to look at this process in more detail. The study of information diffusion distinguishes between two types of contagion processes. One, called Independent Cascade Model, where each node in the infected stage can influence its susceptible neighbors with an equal rate of success. The other, called the Linear Threshold Model, where a node is infected depending on how many of its neighbors are already infected. If the rate of infection in the node’s neighborhood exceeds a certain threshold, it transitions into the infected stage (Hui et al 2010; Watts 2002). We will focus on the linear threshold model as suits the best for describing real-life phenomena of information contagion and is observable in a wide range of social phenomena that involves a collective action (Shelling 1960; Granovetter 1978). In this model the individuals are more likely to commit to a certain belief or action once a sufficient number of their neighbors have also committed to the same thing. It has been shown that when the nodes from the same group are densely interconnected, they propagate information with high trust (Hui et al 2010) and information is more likely to spread through the whole cluster during a certain period of time (Young, 2002) as the “conversion” threshold for each participant is exceeded. These results go in line with research in diffusion of innovations (Rogers, 1995) where the importance of social networks for information contagion processes was emphasized in that individuals’ influence over each other plays an important role in product adoption. Therefore, as it’s been shown earlier, closely-knit groups are much more conducive for initial information contagion within the nodes that belong to the group, because the threshold for adopting a certain trend or behavior is exceeded. The conditions for information contagion are even better when the focus is made on so-called “early adopters”, who have a lower threshold (Gladwell 2000). If these individuals form a tightly-knit group connected to other communities, the rate and the reach of information contagion will increase, while its cost will be reduced because less seeding is required.
Moreover, it has been shown that epidemic in SIRS models can be more persistent when individuals possess memory (Dodds & Watts, 2005) and the epidemic threshold decreases (Zhong et al 2011). This is due to the fact that repetitive information contagion is more efficient when individuals retain the impulses from previous encounters for a long enough time, so that when then next encounter occurs it is combined with the ones “memorized” and together they exceed the threshold. Also, for SIS models, the longer the “infected” stage, the more prevalent is the spread of the epidemic (Xu et al 2008). It should be noted, however, that some other studies in viral marketing showed that probability of contagion decreases with repeated communication (Leskovec et al 2007), possibly due to the fact that each message repeated from the same source loses its authority and novelty over time.
It should be noted, however, that the community structure and the overall network structure plays an important role in how fast information spreads through the network. While it has been shown that the presence of a giant component (a group that connects most of the nodes in a network) is crucial for informational cascades to occur (Watts 2002), the increasing density of connections will lead to the situation where the proportion of nodes that adopted a certain trend in one’s neighborhood does not exceed the threshold necessary for adoption. In other words, the more people we know, the more people we need in our surrounding to carry a specific message for us to want to take a notice of it. This has also been independently confirmed by Keeling (1999) who has shown that increasing clustering stifles epidemic spread in networks.
Therefore, once the group reaches a certain level of connectivity it is not as effective in propagating information, at least when there’s a certain threshold for information adoption.
It is, however, important to mention that these results were found to be valid for SIR epidemic models where the nodes, once recovered, do not transition back into susceptible state. Other research on this subject has shown that as the shortcut density in a scale-free network increases (bringing it closer to random degree distribution), the system goes through a phase transition where the infection level shifts from a low endemic level to high-amplitude oscillations for SIRS model. (Kuperman & Abramson 2001). In this case, the negative effects of increased clustering are neutralized by a higher overall rate of adoption, because the nodes can transition back to susceptible state, and the threshold necessary for rapid contagion is exceeded. At the same time, according to Kuperman & Abramson (2001) once the network is more regular and has a more prominent community structure, the epidemic has much more capacity to stay at a low endemic level, maintaining its presence in a localized way.
Another research has shown that random links facilitate rapid communication of ideas in network, and that the community structure accelerates the diffusion due to the presence of redundant cohesive relationships and it is in general beneficial for promoting diversity of knowledge across communities (Lambiotte, R., & Panzarasa, P. 2009).
These results were confirmed by Yan et al (2008) who showed that for information to propagate in a viral way (giving rise to short-lived trends and rumors) the community structure of the network has to be less prominent (although still existent). In this case the information will propagate through the network quickly in waves or spikes of activity. Similar findings were demonstrated by Liu & Hu (2005), who found that community networks have broader degree distribution than random network, a lower epidemic threshold and more prevalence to keep an outbreak endemic. Random networks have a higher threshold for epidemic outbursts, but once it happens it’s more likely that it will be global than in scale-free community network. Zhou et al (2008) showed that the total number of infected nodes can be higher in random networks than in scale free networks and it increases with the rise in degree.
Similar findings can be found in marketing: Leskovec et al (2007) demonstrated that viral strategies work much better if they originate in densely connected communities, which then spread information across the network at large. Research on information contagion in online social networks Digg and Twitter have also confirmed that when a certain piece of information originates in a tightly-knit densely interconnected community, it can go viral in that community much faster than in less densely connected communities (Lerman & Ghosh, 2010). At the same time, if the communities are less densely connected within, but are better connected to each other, the contagion rate will be slower, but will have a better global reach.
To summarize, most research shows that when information originates in a densely-knit community, it is more likely to spread through the rest of the network that community belongs to. If the community has high connectivity and random degree distribution, more nodes will need to be seeded with information for it to propagate initially, but once the threshold is exceeded, the contagion will happen more rapidly within that community. Memory of previous encounters plays an important role in decreasing the threshold as well as the structure of the network – it should be dense enough for information contagion to be global, and not too dense for each impulse to retain relational relevance.
In order for information contagion that occurred within a community to then propagate through the whole network, it has to have visible community structure but at the same time have a high number of random shortcuts between the communities. Less prominent community structure and more random shortcuts are more likely to produce a short-lived global contagion. More prominent community structure and less random shortcuts are more likely to produce a long-lived contagion that stays endemic across the whole network or in separate communities. A certain degree of connectedness is still necessary though for information epidemic to occur at all.
The importance of random shortcuts within the communities as well as across the communities for synchronized information contagion should be emphasized. Cummings et al (2004) demonstrated using the data on Dengue fever in Thailand that there’s periodicity in epidemic spread. It has also been shown that for SIRS model the amplitude of contagion increases (as well as the speed and prevalence of epidemics) with the number of random shortcuts in network (Kuperman & Abramson, 2001). Further research have shown that small-world wirings enhance synchronizations as compared to regular topologies and that the addition of random links between nodes further enhances the network synchronization (Barahona & Pecora 2002). Synchronization is further boosted if the wirings between the nodes are asymmetric, that is the random links are made between the nodes with a varying degree (Boccaletti et al 2006). Furthermore, it has been shown that chaos produces local oscillatory patterns (within communities), while asymmetric coupling with varied weight distribution (that is related to the overall topology of the network) suppresses this chaos and instead turns the whole system into periodic sync (Bragard, 2007). In other words, disassortative networks synchronize more easily, while assortative ones are better at percolating (Newman 2002b). This is again an indication that the overall structure of the network defines how information contagion occurs. If the network is assortative, with clearly defined communities that are connected together through a few, but relatively short paths (a typical small-world network), the contagion may occur, but the global synchronization is less likely to happen. If the same network is randomized to the point that it becomes more disassortative, that there are more random shortcuts between the communities, and that the nodes with different degree are connected together, the contagion will occur much more rapidly and in a synchronized way, although it may be more short-lived.
This brings us to the importance of brokers or lynchpins in social networks for information contagion. Brokers connect different communities together, which would not be connected otherwise and it is a well-known fact in business that they are crucial to viral information contagion. Stonedahl et al (2010) demonstrated that the optimal viral strategy in Twitter network was to seed information to brokers (nodes with high degree and low clustering). The importance of brokers is also often demonstrated in network science. The nodes with the highest betweenness centrality, which occur most often on the shortest paths between random pairs of nodes in a network, were shown to be crucial for information dissemination (Freeman, 1977; Brandes, 2001). The nodes with the highest betweenness centrality or the brokers are the ones that contribute to forging the random shortcuts between communities mentioned earlier in this paper. Therefore, the most efficient strategy for information dissemination would not only be focusing on seeding information to tightly-knit groups and randomizing the network structure, but also seeding the information to the nodes, which have the highest betweenness centrality, so that they help spread information across the network. This should only be done if the model of contagion follows SIRS stages, meaning that the nodes can transition into susceptible state again. Otherwise preliminary seeding of information to the nodes with the highest betweenness centrality may render them removed (R stage) and may stifle communication between the communities. In the latter case a more efficient strategy could be to instead focus on communities, which have the highest betweenness centrality or that are connected to such nodes.
Brokers are different from hubs in the way that they do not necessarily have more connections, but, rather, connect different communities together. Seeding information to the brokers is more efficient, as they help it spread through the whole network. It has also been shown that hubs are not as efficient as previously thought for viral marketing, because there’s only a certain amount of influence that a hub can exert in its network (Leskovec et al 2007).
Now that we identified the structure of the network that’s most conducive for synchronized information contagion (the presence of communities linked by random asymmetric shortcuts) and the initial seeding strategies (tightly-knit groups, “early adopters”, and the nodes with the highest betweenness centrality) it is time to turn to the essence of the network, that is, the connections themselves.
4. Viral Communication
When we talk about social networks, we talk about nodes and edges. However, a network, in a static state, is a representation of interactions between the nodes over a certain period of time (Newman et al 2006; Watts 2010, Friedenberg & Silverman 2011). When we talk about information contagion strategy based on that representation, we can be sure more or less about the nodes that are present in the network (on the basis of their belonging to the target group, for example), but the edges are much more difficult to grasp.
What is the nature of the node’s existing relationship, prior to information contagion occurs?
If we take a Facebook network, for example, then the nodes will represent the people and the edges will represent who added who as a friend. However, the amount of communication that happens across the network, the intensity of each connection is much harder to grasp. Moreover, whether information will spread over the network depends on how much related it is to the purpose of that particular network to hold the nodes together. It is hard to say whether a network based on a shared political interest will be interested in a new fashion trend. Or whether a network of researchers in the field of social sciences would be interested in political activism. When we talk about information contagion within a network, we are talking about a multiplicity that was formed for a different purpose and with a different agenda than that of the information which would be communicated. So some of the nodes will a priori be immunized to that information and the resulting structure will in fact be defined by the willingness of the nodes to take on the information and pass it further.
In other words, the content of information determines how it will spread in the network.
It has been shown that news, for example, spread across social networks much easier than topic-based discussions, which are determined by functional relationships – who works for who, who is a friend of who, etc. (Aral et al 2007).
Therefore, information will only be contagious if the nodes a priori are not immunized against it. For a message to go viral it should be compelling to share.
How can we ensure that the community is not immunized against information before the contagion starts?
One of the ways, if the communities already exist, it can be useful to identify a certain purpose, reason or agenda that brings the members of that community together. One of the ways to do that is to build a “mental map” (Carley & Palmquist 1992; Carley 1997), which would give an idea of sentiments in a group. Then one of the possible strategies to disseminate information would be to find the relation between this information and the “mental map”, that individuals would want to absorb this information and propagate it further (Paranyushkin, 2011b). That could imply changing the content of information so that it appeals to the target group, while retaining the core message. Political forces, for example, often appeal to the clearly identified needs of the population in order to get its support. A recent study of inauguration speeches of two Korean presidents has shown that the network visualization of their inauguration speeches produced the concept map that was closely related to the current political agenda in the country (Chung & Park 2010).
Identifying the interests of the target communities in order to proliferate a certain message is popular tactics in viral marketing campaigns. That could also imply finding the communities, which are the least immunized to the forthcoming information. An example can be “early adopters” communities (Gladwell 2000), but also any group to which the information can have a tangible added value. A possible measure of the informational “added value” to a group could be a decrease in entropy or ambiguity (Snow 2010). If we model the information available to a group as a network of inter-related concepts (Latour 2005; Carley & Palmquist 1992; Foucault 1977), then the entropy of such network will decrease as its degree distribution shifts from random (Poisson) distribution towards that of the scale-free, following a power law (Bianconi 2007; Passerini & Severini 2008). That is, a message will have the highest informational value when it weaves its discourse into the discourse of the group in such a way that the overall connectivity and regularity of the resulting network is decreased. In practical terms this has very interesting consequences: a message that can bridge a “structural hole” or an existing gap in the knowledge network (Burt 2004), will be considered of a less informational value than the message that produces a new one. The recent study of the London riots rumor propagation conducted by The Guardian and a team of researchers (Dant & Richards 2011) demonstrated that the most long-lived rumours were the ones that originated from questions (thus, creating structural holes), which then created a certain antagonism (supporting and denying statements) in the Twitter community (Fig 5). It is of course arguable whether such information is valuable in the long term, however, in the context of viral marketing where short-term results may be more desirable such approach can be of value.

Figure 5: Rumour spread on Twitter network (by Guardian)
Another related strategy that can produce structural holes within a community is to introduce fiction into the mental map of the target community. Fiction can work as a binding glue for individuals that would not normally interact together. Adding it as an extra layer and weaving it into what is considered by the community to be real may decrease the entropy and thus prepare the resulting network for the forthcoming informational epidemic.
Such strategy is often used in computer game design to make them more engaging for players (Schell 2008). Specifically it is recommended to create a successful story with simple rules of operation and several external motivators for progress in order for people to be involved longer in the process of playing. Adding an element competition (e.g. leader boards) into the social interactions between players is also considered to be an effective strategy for engaging the players.
What happens when fiction is introduced into the social field is that the already existing information is recontextualized. Fiction can offer a different basis for connectivity between the members and reduce the level of immunization within the network to the certain messages that skillfully utilize fiction in order to propel through the network. There are many examples of it in everyday life. A popular book called The Game describes a strategy used by so-called “pick-up artists” of recontextualizing the situation in order to interact with strangers (Strauss 2005). Elie Ayache, one of the writers active in the field of speculative realism, talks about unpredictable events as a case of changing the context (Ayache 2010). Any new piece of information that takes over a large group should be unpredictable, that is the interest in it. Therefore, if a message carries with itself a statement that has the capacity to go beyond what’s expected, it will reduce immunological barriers within the network.
We can summarize these findings on the workings of contagion and its relation to community structure as follows. We have shown above that an effective strategy for information contagion is to target several distinct communities first and then let them spread information across the whole network. It should be taken into account, however, what network structure these distinct communities have, as well as the structure of the whole network at large.
Communities that have random structures are harder to enter (requires more nodes to be “seeded” initially), but once the threshold is exceeded, they are more likely to spread information quickly within. Whether the information will spread globally across the whole network is another matter, which depends on how well the particular communities are embedded into the larger structure. If they have lots of shortcuts and links to other communities, then information is more likely to go viral. If the communities are many and separated from each other, the initial wave might dampen too quick for the message to go through to all of them.
It should be noted that the more interconnected is the community, the more short-lived the epidemics within that community will be. Therefore, the momentum or regular rhythm of communication is important in order to ensure that a certain message propagates continuously through the network.
Therefore, we can see that random networks with Poisson degree distribution require more nodes to be “infected” initially, but will then spread the contagion across the whole structure. While scale-free (small-world) networks have a lower threshold for contagion, but the contagion is less likely to be global. The community structure allows to maintain contagion endemic and randomness helps it spread globally.
So the best strategy for producing informational cascades in network is simultaneous seeding of information into densely interconnected groups and randomization of the network structure, but only temporarily, so that it can maintain its small-world properties. This way random formation will give rise to quick global bursts, while small-world structure will ensure that information is sustained in the network on some endemic level within communities.
5. Practical Applications
We will now discuss how the strategy outlined above can be applied in practice using the example of a promo campaign in a social network and a live event designed to bring people together temporarily around a certain theme.
Facebook Promotion Campaign
The first example of applying this strategy is an online campaign to promote a travel guide to Russia page on Facebook ( http://facebook.com/waytorussia ). Our goal was to increase the rate of Likes for this page and to raise visibility of the page by increasing the number of interactions for each of the page’s post (which means that more of the Page’s “fans” on Facebook would see it).

The experiment was done during the period of 1 October 2011 to 30 November 2011. The control period was 1 August 2011 to 30 September 2011 where we did not utilize the strategy, however the rate of posting the updates was more or less the same.
Our approach would make use of the four elements of the strategy outlined in Part 2 of this paper.
Identifying the initial target groups. The current page was analyzed as of 1 October 2011 to identify the main age and interest groups. We found that 44% of the Page’s audience were males and females aged between 25 and 34, 15% of them were based in Moscow and most of them used Facebook in English. Using this information we identified that the most interesting target group in terms of the possibilities for spreading the information posted on our Facebook page were the expats living in Moscow. They are more likely to be connected between each other than the others and also have an extensive reach both inside Russia and outside of the country providing the random connectivity needed to communicate our messages across the whole network.
All the messages we posted during the next two months would necessarily be of interest to that group in order to increase the chances that they would be willing to pass them on further across their networks.
Making the network more interconnected. This was achieved through several means. During October we were creating more shortcuts between different “fans” of the page. In order to do that a personal profile was created on Facebook for WayToRussia guide (see the snapshot of the network on Fig 2). We would then “friend” the most active fans of WayToRussia.Net page and introduce those of them who could be helpful to each other for planning their trip to Russia. This strategy allowed us not only to help people find each other but to also increase the connectivity of the network of “fans” for the Page, therefore increasing the information dissemination capabilities of the network. This same profile was also used to “Like” the posts on the page, in order to increase its visibility on Facebook. As can be seen from Fig 2 many nodes in the network are disconnected from the main component making it very hard for information to propagate. Therefore one of the goals prior to information campaign is to make it more connected by introducing disconnected nodes to each other.
During November we additionally placed an ad on Facebook that was shown to the friends of people who were already “fans” of the Page. Those who engaged through this ad had at least one friend who was already engaged with WayToRussia before, thus helping us build a more interconnected community.
Introducing several lynchpins into the community. The personal profile of Way to Russia had the highest betweenness centrality in the network, along with the page admin’s profile. It is well known that Facebook follows so-called EdgeRank in order to determine which posts to display at the top and one of the defining factor is the number of interactions with that post among the user’s friends. Therefore, all posts were “liked” or shared and commented by these two profiles in order to increase visibility in the network.
The content of the message has to be compelling enough for it to be shared further. We found that visual material along with the statements formed as questions were the most effective. This is consistent with our propositions in Part 2 of this paper: the message should stay out, decrease entropy, make a link to the existing mental set of the group while offering a certain novelty, and ask for a response. An image accompanied with a question is an effective medium to combine all of these.
The results of this strategy are displayed below (Fig 7 and Fig 8).
 
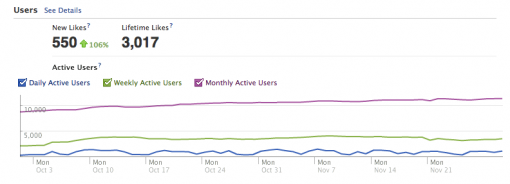
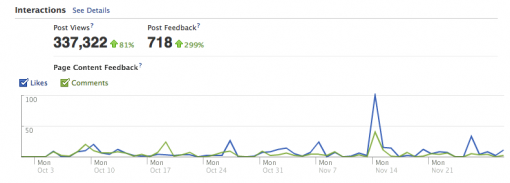
We found that the number of post views increased by 81% comparing to the control period (1 August – 30 September 2011), post feedback increased by almost 300%, and 550 people Liked the page comparing to 220 during 1 August – 30 September 2011. 176 of these new likes were made through the advertising, the rest 374 were made through the increased interaction with posts.
Therefore this strategy was successful in promoting a Facebook page and increasing the level of engagement for its users.
Live Event Organization
Most of the events have a very disrupted social structure: people come in small groups who don’t know each other. What we call the “good vibes” or the “right atmosphere” cannot be sustained without people passing it on to each other. Therefore, the first step in making a memorable event is to make the social structure within the event interconnected, to provide a sort of social glue that would bring people together and encourage them to make random connections to those outside of their immediate surrounding.
On the 9th of December 2011 we organized a live event in Berlin called “Magic Movement”. We were interested to see if the strategy outlined above for improving information contagion can bring a group of people together temporarily. Our idea was to make a theme for the party, a kind of story or a unifying fiction that would bring people together on a temporary basis. We decided to call it “Magic Movement” and to introduce the dress-up theme of “Magic” in order to invite people into fiction from the moment they enter the space. Another strategy we wanted to use was to introduce several ongoing activities, which encouraged people to interact with those outside of their circles. This was done through distributing fortune cookies with tasks that were to be given by the person who received them to any random stranger. We also had several activities within the space that involved temporarily bringing together several people from different groups that did not interact with each other before and introducing them to one another through playful non-obtrusive interaction. We also made sure to invite several groups of people who knew each other, in order to increase inter-group communication, as well as the “lynchpins” who’d be likely to know some people from different groups. Finally, dancers were planted into the audience to encourage a slightly higher than usual level of movement in order to ensure there was a rhythmical influx of the original “fiction” into the atmosphere.
Schematically the process we envisioned for that event is represented on Fig 9 below:
The event was attended by more than 150 people and from what we could gather later most of the participants were really satisfied with how it went. We also compared this event to the other ones of similar size organized in the same club before and found that the alcohol sales in our event were about 30% higher than normal and the party lasted about 7 hours instead of the standard 5 for that venue. While these may seem dubious indicators of success to some, they are also the only quantitive measures for event’s success that were available to us at the time.
6. Conclusion
We have reviewed above the research on informational cascades and epidemics in networks. We found that the structure of the network can affect the dynamics of the contagion dramatically.
First of all, the network should have a giant component (most of the nodes belonging to a connected component) in order for the contagion to occur at all. The structure of that component will determine the life span of the contagion, its ability to disseminate a message through the whole network, and the threshold required for contagion to occur.
We found that the networks where most of the nodes have more or less similar number of connections (Poisson distribution of degree) require more nodes to be “infected” initially for the contagion to occur, but then are more likely to proliferate the contagion through the whole network in a synchronized fashion. Such networks are prone to periodical information cascades (simultaneous distribution of information among many nodes periodically), however, once they become too densely connected the efficiency of contagion will decrease due to a high number of influential nodes in one’s surrounding (so more nodes are required to change one’s opinion). At the same time, the life span of informational contagion in such networks is low and they require continuous stimulation in order to maintain interest.
Scale-free networks (where distribution of degrees among nodes follows a power law), which are typical for real-life networks, require less nodes to be “infected” initially for information to spread through the whole network. However, the speed of contagion would be lower than in the random networks and periodical informational cascades are less likely to occur. Therefore to ensure the high rate of contagion it is necessary that it originates within a few clusters (subgroups) that are more densely connected (preferably the subgroups that have random network structure). The information will then spread across the whole network across the meta-network formed by these communities between one another. To ensure that the rate of propagation is high, there should be a higher level of random connections between these communities, facilitated by both the behavior of the members and the lynchpins (members that connect different communities together).
Finally, the message itself should be viral in that it has the embedded capacity to recreate itself. This can be done through formulating it in a way that engages the recipient to continue the interaction (e.g. forming it as a question). This message should also be designed it in a way that acknowledges the existing mindset of the key lynchpin members and target groups while proposing a novelty that would be compelling enough for people to share.
When choosing the effective communication strategy it is also important to choose which groups to address first. We have also shown that the most effective immunization strategy was to leave an equal number of susceptibles in each subgroup. Therefore the message should be carefully crafted in such a way that it would not create any antagonism within several groups, which would then pass it on to the rest (towards which the message then be antagonistic to stir more reaction). Such viral design would allow for the message to spread quickly within the initial seeding groups and be more effective on the intra-group level due to its controversy. The design of the message would impose a kind of meta-structure on top of the already existing social one where every member should choose whether to side with the message or not and that choice would also be related to the reasons why the group they belongs to maintains its ties. In other words, nationalistic, sexist, racist and blunt statements phrased as implicit questions spread much better because they already carry a certain antagonistic dichotomy within their design and provoke one for a response.
These results have been demonstrated using the practical examples of promoting a company page on Facebook and organizing a live event. We have shown that the initial modification of the network to make it more densely connected followed by targeting specific groups and embedding the mechanisms of increased random interaction allow for a more vibrant community where the members are sharing information and interacting more actively.
We believe that these findings can also be useful for communities to build preventive measures against informational warfare while maintaining the ability for a collective action. A message that is not relevant to the purpose that’s holding the community together is not likely to be disseminated. Therefore, the structure of the community should be based on some common understanding of truth (or fiction) where every interaction that happens within such network only reaffirms the founding principle. If the founding principle is the number of “likes” the person received on Facebook, such network is very easy to compromise. However, if the founding principle is “the joy of encounter that survives its expected end” and “the density of ties at the core” (Invisible Committee 2008) then such community will be much harder to compromise.
Maintaining a certain degree of antagonism within tightly knit groups within the community is also an effective immunization strategy against external influence. If the groups maintain a high number of random links and shortcuts to each other, occasionally exchanging the members (thus, each group’s ideology also changes) they will still be structurally capable for a collective action, however, the reason for such action will be much harder to impose from the outside, due to the constant polysingular nature of the network. A community that has multiple centers, which are specific in terms of the purpose that brings them together and yet where each member is ready to shift and be alone or join another center at any moment of time. Such community maintains the social polysingularity necessary for a vibrant and active interaction within. It is also prepared for a collective action and immunized against the external influences, which are not relevant to the purpose that holds the community together.
In this context it is appropriate to mention Gregory Bateson’s research on sustainable communities in Polynesia (Bateson 1973). During his anthropological research he discovered the tribes that followed what he called reciprocal model of the relationship. Members of this community would constantly exchange roles (control – submission, strong – weak) never allowing the conflict to escalate or for dichotomies to increase above a certain threshold. This way the heterogeneous structure was retained among with the proactive groups that would initiate change. However, the constant rotation of members in these groups ensured that contagion never reaches a permanent level and instead stays on a lower endemic level maintaining the group’s capacity for a collective action but never to the point that would be self-destructive for the group.
References
Aral, S., Brynjolfsson, E., & Van Alstyne, M. (2007). Productivity Effects of Information Diffusion in Networks. Business.
Ayache, E. (2010). The Blank Swan: The End of Probability. Wiley
Barahona, M., & Pecora, L. M. (2002). Synchronization in Small-world systems. Physical Review Letters, 89(5), 54101. APS. Retrieved from http://link.aps.org/doi/10.1103/PhysRevLett.89.054101
Ball, F. (1997). Epidemics with two levels of mixing. The Annals of Applied Probability, 7(1), 46–89. Institute of Mathematical Statistics. Retrieved from http://projecteuclid.org/euclid.aoap/1034625252
Ball, F., Neal, P., & Lyne, O. (2010). Epidemics with two levels of mixing. MOdelling Complex Systems, University of Manchester. Institute of Mathematical Statistics. Retrieved from http://projecteuclid.org/euclid.aoap/1034625252
Bastian, M.; Heymann, S.; Jacomy, M.; (2009). Gephi: An Open Source Software for Exploring and Manipulating Networks. Association for the Advancement of Artificial Intelligence
Bateson, G. (1973). Steps to an Ecology of Mind. (C. P. Co, Ed.)The Western Political Quarterly (Vol. 26, p. 345). Aronson. doi:10.2307/446833
Barabasi, A.-L., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286(5439), 11. AAAS. Retrieved from http://arxiv.org/abs/cond-mat/9910332
Bianconi, G. (2007). The entropy of randomized network ensembles. Europhysics Letters, 81(2), 6. Elsevier. Retrieved from http://arxiv.org/abs/0708.0153
Bikhchandani, S., Hirshleifer, D., & Welch, I. (1992). A theory of fads, fashion, custom and cultural change as informational cascades. Journal of political Economy, 992–1026. JSTOR. Retrieved from http://www.jstor.org/stable/10.2307/2138632
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang, D. (2006). Complex networks: Structure and dynamics. Physics Reports, 424(4-5), 175-308. doi:10.1016/j.physrep.2005.10.009
Bragard, J., Vidal, G., Mancini, H., Mendoza, C., & Boccaletti, S. (2007). Chaos suppression through asymmetric coupling. Chaos (Woodbury, N.Y.), 17(4), 043107. doi:10.1063/1.2797378
Brandes, A. (2001). Faster Algorithm for Betweenness Centrality. In Journal of Mathematical Sociology 25(2):163-177
Burt, R. S. (2004). Structural Holes and Good Ideas. American Journal of Sociology, 110(2), 349-399. The University of Chicago Press. doi:10.1086/421787
Callaway, D. S., Newman, M. E. J., Strogatz, S. H., & Watts, D. J. (2000). Network robustness and fragility: Percolation on random graphs. Physical Review Letters, 85(25), 5468–5471. APS. Retrieved from http://link.aps.org/doi/10.1103/PhysRevLett.85.5468
Carley, K and Palmquist, M (1992). Extracting, Representing, and Analyzing Mental Models. Institute for Software Research. Paper 40.
Carley, K. (1997). Extracting Team Mental Models through Textual Analysis. Journal of Organizational Behavior
Chung, C. J., & Park, H. W. (2010). Textual analysis of a political message: the inaugural addresses of two Korean presidents. Social Science Information, 49(2), 215-239. doi:10.1177/0539018409359370
Cummings, D. A. T., Irizarry, R. A., Huang, N. E., Endy, T. P., Nisalak, A., Ungchusak, K., & Burke, D. S. (2004). Travelling waves in the occurrence of dengue haemorrhagic fever in Thailand. Nature, 427(6972), 344–347. Nature Publishing Group. doi:10.1038/nature02226.1.
Dant, A & Richards, J (2011).Behind the rumours: how we built our Twitter riots interactive. The Guardian datablog. http://www.guardian.co.uk/news/datablog/2011/dec/08/twitter-riots-interactive
Dodds, P. S., & Watts, D. J. (2005). A generalized model of social and biological contagion. Journal of theoretical biology, 232(4), 587-604. doi:10.1016/j.jtbi.2004.09.006
Foucault, M. (1977). The Confession of the Flesh interview. In Power/Knowledge Selected Interviews and Other Writings (ed Colin Gordon), 1980: pp. 194-228.
Freeman, L. (1977). A Set of Measures of Centrality Based on Betweenness. Sociometry
Vol. 40, No. 1 (Mar., 1977): 35-41
Friedenberg, J., & Silverman, G. (2011). Cognitive science: an introduction to the study of mind. Sage Publications.
Gabdulkhaev, B. G. (2005). Polysingular integral equations with positive operators, 49(11), 2005.
Gladwell, M. (2000). The Tipping Point: How Little Things Can Make a Big Difference. Little Brown, New York
Granovetter, M. S. (1978). Threshold Models of Collective Behavior. American Journal of Sociology, 83(6), 1420. The University of Chicago Press. doi:10.1086/226707
House, T., & Keeling, M. J. (2009). Household structure and infectious disease transmission. Epidemiology and Infection, 137(5), 654-661. Cambridge University Press. Retrieved from http://dx.doi.org/10.1017/S0950268808001416
Hui, C., Goldberg, M., Magdon-Ismail, M., & Wallace, W. A. (2010). Simulating the diffusion of information: An agent-based modeling approach. International Journal of Agent Technologies and Systems (IJATS), 2(3), 31–46. IGI Global. Retrieved from http://www.iamcindyhui.com/wp-content/pubs/Hui_Paper_IJATS_Simulating the Diffusion.pdf
Invisible Committee (2008). The Coming Insurrection, From http://tarnac9.wordpress.com/texts/the-coming-insurrection
Ioffe, J (2011). Net Impact: One man’s cyber-crusade against Russian corruption. New Yorker, April 04 2011
Keeling, M. J. (1999). The effects of local spatial structure on epidemiological invasions. Proceedings. Biological sciences / The Royal Society, 266(1421), 859-67. doi:10.1098/rspb.1999.0716
Kuperman, M., & Abramson, G. (2001). Small World Effect in an Epidemiological Model. Physical Review Letters, 86(13), 2909-2912. doi:10.1103/PhysRevLett.86.2909
Lambiotte, R., & Panzarasa, P. (2009). Communities, knowledge creation, and information diffusion. Journal of Informetrics, 3(3), 180–190. Elsevier. Retrieved from http://www.sciencedirect.com/science/article/pii/S1751157709000248
Latour, B. (2005). Reassembling the Social: An Introduction to Actor-Network Theory. Oxford University Press.
Lerman, K., & Ghosh, R. (2010). Information contagion: An empirical study of the spread of news on Digg and Twitter social networks. Proceedings of 4th International Conference on Weblogs and Social Media (ICWSM). Retrieved from http://www.aaai.org/ocs/index.php/ICWSM/ICWSM10/paper/viewPDFInterstitial/1509/1839
Leskovec, J., Adamic, L. A., & Huberman, B. A. (2007). The dynamics of viral marketing. ACM Transactions on the Web (TWEB), 1(1), 5. ACM. Retrieved from http://dl.acm.org/citation.cfm?id=1232727
Liu, Z., & Hu, B. (2005). Epidemic spreading in community networks. Europhysics Letters, 72(2), 315-321. IOP Publishing. doi:10.1209/epl/i2004-10550-5
Mandelbrot, B (1999). Multifractal systems and 1/f noise.
Marvel, S. a, Kleinberg, J., Kleinberg, R. D., & Strogatz, S. H. (2011). Continuous-time model of structural balance. Proceedings of the National Academy of Sciences of the United States of America, 108(5), 1771-6. doi:10.1073/pnas.1013213108
Newman, M. E. J. (2002a). The spread of epidemic disease on networks.
Newman, M. E. J. (2002b). Assortative mixing in networks. Physical Review Letters, 89(20), 5. American Physical Society. Retrieved from http://arxiv.org/abs/cond-mat/0205405
Newman, M. E. J., Barabasi, A.-L., & Watts, D. J. (2006). The structure and dynamics of networks. Princeton University Press. doi:10.1073/pnas.0912671107
Paranyushkin, D (2011a). Inclusive Exclusivity of the “Dynamique d’Enfer”: How to Build Open and Innovative Cultural Networks. Under review.
Paranyushkin, D (2011b). Topological Representation of Narrative Structures using Text Network and Graph Analysis. Under review.
Pariser, E. (2011). The Filter Bubble. Penguin Press.
Passerini, F., & Severini, S. (2008). The von Neumann entropy of networks. Physics, (12538), 5. Retrieved from http://discovery.ucl.ac.uk/404737/
Pastor-Satorras, R., & Vespignani, A. (2000). Epidemic spreading in scale-free networks, 13. doi:10.1103/PhysRevLett.86.3200
Phillips, S. (2007). A brief history of Facebook. The Guardian, (January), 2011-2011. Retrieved from http://www.guardian.co.uk/technology/2007/jul/25/media.newmedia
Rogers, E. M. (1995). Diffusion of innovations. Free Press. doi:10.1525/aa.1963.65.5.02a00230
Schell, J. (2008). The Art of Game Design: A book of lenses. Morgan Kaufmann.
Schelling, T. C. (1960). The Strategy of Conflict. Harvard University Press Cambridge Mass (Vol. 2, p. 309). Harvard University Press. doi:10.1177/002200275800200301
Snow, A. (2010). Ambiguity and the value of information. Journal of Risk and Uncertainty, 40(2), 133-145. doi:10.1007/s11166-010-9088-7
Stonedahl, F., Rand, W., & Wilensky, U. (2010). Evolving Viral Marketing Strategies. Learning.
Strauss, N. (2005). The Game: Penetrating the Secret Society of Pickup Artists. IT Books.
Strogatz, S.H., 1994. Nonlinear Dynamics and Chaos Steven Henry Strogatz, ed., Perseus Books.
Varela F.G., Maturana H.R., Uribe R. (1974). Autopoiesis: The organization of living systems, its characterization and a model. Biosystems, Volume 5, Issue 4, pages 187-196
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. (M. Newman, A.-L. Barabási, & Duncan J Watts, Eds.)Nature, 393(6684), 440-2. Nature Publishing Group. doi:10.1038/30918
Watts, D. (2002). A simple model of global cascades on random networks. Proceedings of the National Academy of, 99(9), 5766-71.
Xie, J., Sreenivasan, S., Korniss, G., Zhang, W., Lim, C., & Szymanski, B. K. (2011). Social consensus through the influence of committed minorities. Physical Review E, 84(1), 1-9. doi:10.1103/PhysRevE.84.011130
Xu, X.-jian, Peng, H.-ou, Wang, X.-mei, & Wang, Y.-hai. (2008). Epidemic spreading with time delay in complex networks, 1-11.
Yan, G., Fu, Z.-qian, Ren, J., & Wang, W.-xu. (2008). Collective Synchronization Induced by Epidemic Dynamics on Complex Networks with Communities. Science And Technology, 0, 3-7.
Young, H. P. (2002). The Diffusion of Innovations in Social Networks. Economy as an evolving complex system 3, 3(1966), 1-19. Oxford University Press, USA. doi:10.1016/0954-349X(90)90002-P
Zhong, L., Qiu, T., Ren, F., Li, P., & Chen, B. (2011). Time scales of epidemic spread and risk perception on adaptive networks. EPL (Europhysics Letters), 94, 18004. IOP Publishing. Retrieved from http://iopscience.iop.org/0295-5075/94/1/18004
Zhou, J., Liu, Z., & Li, B. (2007). Influence of network structure on rumor propagation. Physics Letters A, 368(6), 458-463. doi:10.1016/j.physleta.2007.01.094