Posted by Nodus Labs | December 10, 2011
Inclusive Exclusivity: How to Build Open and Innovative Cultural Networks
By Dmitry Paranyushkin, Nodus Labs, Published October 2011
Abstract:
In this paper we are looking at the phenomenon of “dynamique d’enfer” typical for cultural networks: a densely interconnected structure with a high innovative potential, high cost of entry, and a certain degree of exclusivity towards new members. After modeling two cultural networks (PAF and INPEX) using real-life data from Facebook, we find that their resulting graph topology, especially among the cliques of the most influential members, is close to that of a random graph. We demonstrate that while this structure is typical for many innovative networks because it allows for the more efficient propagation of knowledge, it also carries certain disadvantages making the networks much more susceptible to node removal, uncontrolled oscillations, and a high degree of exclusivity that leads to stagnation. We then discuss (in the context of cultural networks) the possible strategies to retain these networks’ innovative potential and their capacity for information propagation, while making them less exclusive, more stable, and more heterogeneous. We believe that our approach has a wide range of applications beyond the scope of cultural networks only, and can be useful for designing innovative networks around the principles of openness, collaboration, and sustainability.
Keywords: cultural networks, random graphs, innovation, arts, knowledge, network analysis
1. INTRODUCTION
Marten Spangberg (a dance critic, choreographer, and the director for the MA program in choreography at the University of Dance in Stockholm) writes about cultural networks being much more exclusive than digital communication networks: “In dance networks operate strictly on strategic levels, without any concern for structural or tactical openness or deployment. Networks in the cultural sector are absolutely closed and are all about membership. You have to make yourself worthy of being part, you will have to go through a test, and you have to invest a fair amount on energy in lobby and travel-costs. […] Networks in cultural businesses operate due a mode or production known as “dynamique d’enfer” or dynamics of hell. […] You are responsible for the maintenance of hierarchies, the preservation of an aristocratic society that operates like a flock of vampires, like apologetic blood suckers that obediently confess there compulsive lust. “ (Spangberg 2011).
Rem Koolhaas, one of the world’s most renowned architects, also writes about the “dynamique d’enfer” existing in cultural networks, pointing out their innovative potential: “I asked the director, a brilliant developer with whom we worked closely, why he never said no […] when we came with all our insane proposals […] He said his strategy to succeed into the twenty-first century was to create within a limited territory what he called a dynamique d’enfer – a dynamic from hell, which is so relentlessly complex that all the partners are involved in it like prisoners chained to each other so that nobody would be able to escape. […] What was exciting here was that we introduced buildings on a scale that Europe had almost never seen, therefore we could experiment with completely new typologies.” (Koolhaas 1993).
So, on one side – exclusivity, hierarchies, vampires, prisons, and even the hell itself. On the other side – innovative potential, strength, and success.
While it’s quite a strange combination, it is not a weird feature of the cultural networks, but is also very typical for many innovative organizations especially in hi-tech industries. For example, it is well-known that Apple, one of the most innovative companies in the world, operates on a very secretive basis (The Economist 2007), and that its late CEO, Steve Jobs, was one of the most authoritarian business leaders (Kahney 2008) of all times.
The central question for this research for us is to find out the necessary structural properties and dynamics that allows a cultural network to innovate and to utilize its full creative potential, while staying open and flexible at the same time. We will model our research based on the real-world data from cultural networks, however, we believe that our results will also be useful for any other context where the objective is to innovate and to have a creative approach to one’s professional domain.
Innovation in networks is closely related to the dynamics within them: both for the members and the knowledge that these members exchange. Knowledge diffusion and mobility (Gilbert et al 2001), innovation appropriability, and network stability (created through allowing the old members to leave and the new members to enter the network) are considered to be very important for building innovative networks (Dhanaraj 2008). Besides, the positioning within a network and the ability to replicate new knowledge across the network have significant effects on the organization’s capacity for innovation and performance (Tsai 2001).
Innovation networks can also have very different structural properties ranging from centralized to distributed mechanisms of control, on the one side, and from homogeneous to heterogeneous knowledge resources, on the other (Yoo et al. 2008).
It has also been previously shown that a combination of strong and weak ties (simultaneous maintenance of a strong interconnected core and weakly connected longer-ranging peripheral connections) is vital to network’s innovative capabilities (Capaldo 2006).
It has been shown that the networks where so-called creative reactions among its members are encouraged within the system, have faster rates of introduction of technological innovations (Antonelli et al 2011).
None of these papers, however, give sufficient attention to the actual structural properties of innovative networks, especially in the cultural sector. While it’s been shown that communication and positioning of the nodes in the network is important, there has been little discussion of the most suitable graph topology to allow for innovative potential to be utilized in a sustainable way.
It is our intention, therefore, to address this deficiency through the study of existing cultural networks and their structural properties. We will do that by modeling cultural networks and seeing how they compare to real-life social friends networks in order to expose their structural specificities. We will then apply research from social network analysis in order to see what would be the optimal structure and dynamics to reap the innovation potential of cultural networks: what should be done to encourage participants of cultural networks to exchange knowledge, be open to learn from their external environment, maintain a degree of dynamic stability as well as a mix of short- and long-ranging ties, and for the agents to be able to respond creatively in order to maintain network’s innovative capabilities.
We will use real data extracted from Facebook from two user profiles: one of them is the personal profile of the author of this paper (we will call him Person A) and the other will be called Person B for privacy reasons. We will first import the friends graph for each of these two individuals. We will then import the data for the professional groups they belong to.
Person A is a member of PAF – Performing Arts Forum association, which unites theoreticians, media activists, performance artists, and choreographers active in the European performing arts scene. Person B is one of the founding members of Swedish-based INPEX, founded by Marten Spangberg (who was quoted above in the introduction) with the goal of internationalizing the Swedish dance scene and cultivating “the cultural player’s international relations and the possibility of cooperation” (Inpex 2010).
After a series of operations on these graphs we will compare the resulting structures for these both individuals and see what the structural differences are between their private and professional cultural networks, in order to get a better insight into the properties of cultural networks in general.
Both PAF and INPEX achieved significant local success in their respective scenes, enabling many practitioners to come together, collaborate, create new work, and increase their presence in the European cultural field – all this on a very tight (almost non-existent) budget. Therefore they can serve as models for innovative networks in the cultural field. At the same time we will also attempt to formulate possible problems that may arise for these networks, depending on the dynamics of their future development, and propose several solutions. The reason why both of these networks were selected is that the author has professional affiliations with them, which will hopefully produce more knowledgeable and accurate interpretations of the modeled data.
In order to extract Facebook graph data for each individual and their respective groups, we used netvizz application to extract the data in GDF format (Adar 2006). Once the data was extracted, we used Gephi software (Bastian et al 2009) in order to visualize it as a graph, run the metrics for resulting networks, and filter the results.
We assume here that Facebook more or less mirrors the actual network of acquaintances and collaborators within a professional field from which the data was extracted.
2. MODELING INDIVIDUAL FRIENDS NETWORKS FROM FACEBOOK
We will first model personal friends networks from Facebook for Person A and Person B in order to get a better insight into their structure and compare the resulting structure and metrics to the professional networks they belong to.
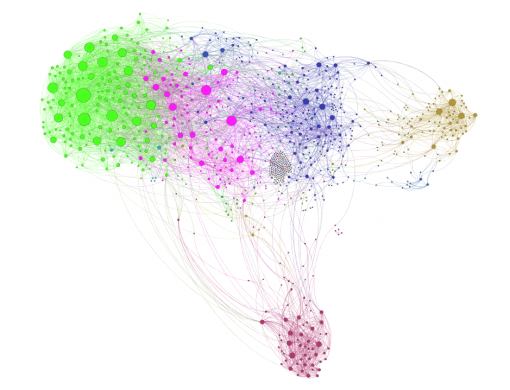
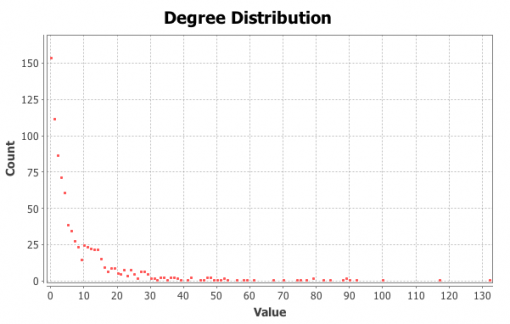
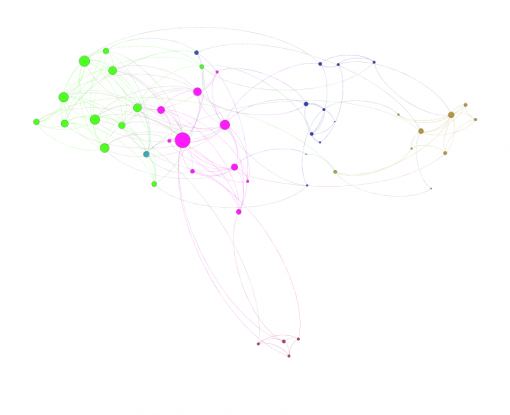
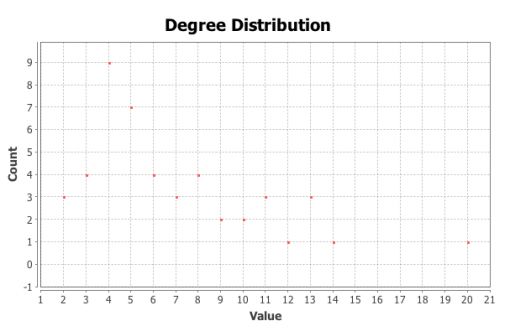
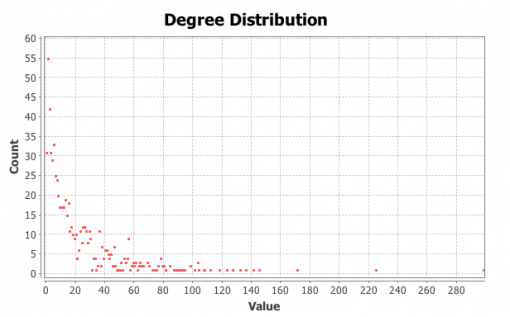
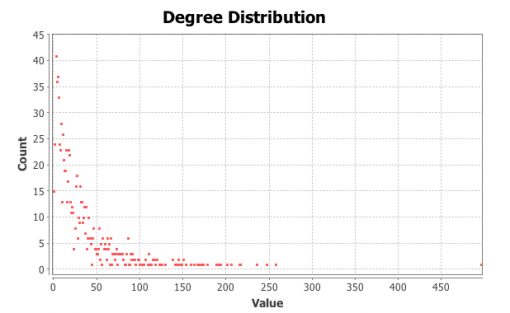
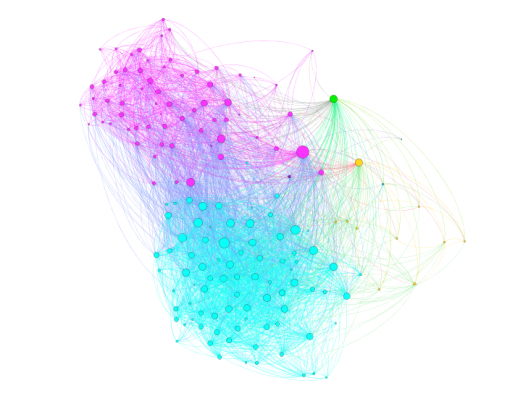
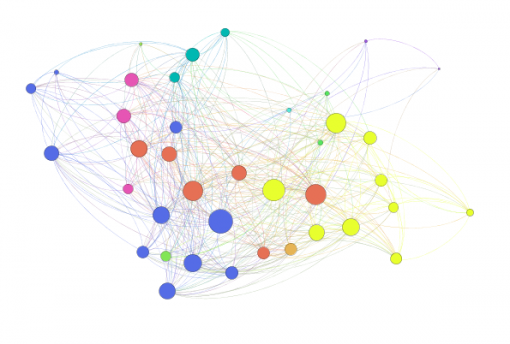
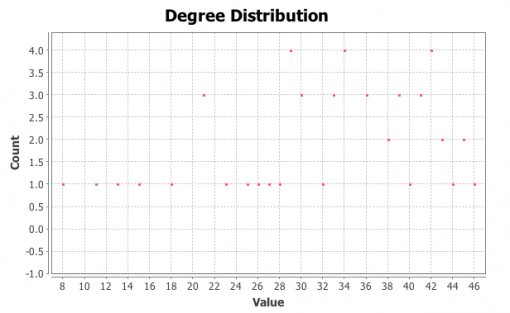
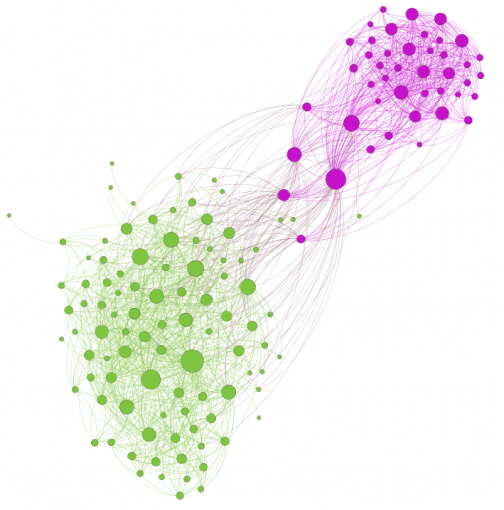
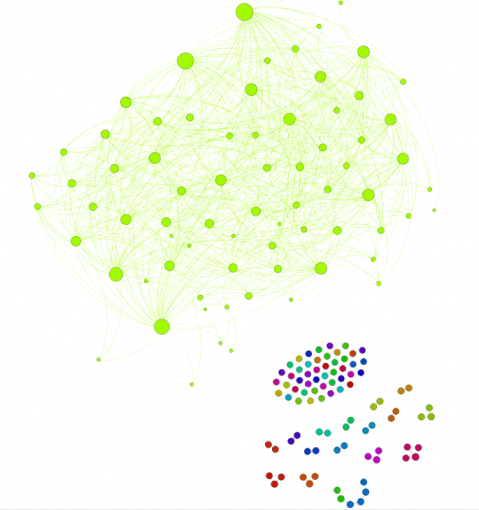
Figures 1 and 3 show the subjects’ respective private social networks. The nodes that are bigger on the graph have a higher degree (the number of connections). The nodes that are more densely related between each other than to the rest of the network are considered to be part of their community (Blondel 2008) and each community has its distinct color. We also show the degree distribution for these networks (Figures 2 and 4), which clearly follows a power law for both individuals: there are a few, but significant number of their “friends” with a lot of connections and most of the other friends have only a few connections. Therefore both of these networks are scale-free, which is very typical for real-life social networks (Newman 2006).
Figure 1: Person A friends network from Facebook
Figure 2: Degree distribution for Person A friends network
Figure 3: Person B friends network from Facebook
Figure 4: Degree distribution for Person B friends network
We then filter all graphs to keep only 5% of the most influential nodes that have the highest betweenness centrality measure. These nodes are more actively engaged in communication within the network and play an important role in connecting our study subjects to all the communities present within the network (Freeman 1977; Brandes 2001).
Figures 5 and 7 show the modified private friend graphs that include only the nodes with the highest betweenness centrality for Person A and B, respectively. Figures 6 and 8 show the new degree distribution. Table 1 shows the main metrics for both networks.
It can be seen that even when we isolate the most influential members around the individual, the structure of the friends network does not drastically change. It is a little bit more dense and interconnected, but the degree distribution of the connections between the most influential members still follows a power law (a few, but significant number of nodes has most connections in the network), so the resulting networks are scale-free.
Figure 5: Person A most influential friends on Facebook
Figure 6: Person A degree distribution for most influential friends on Facebook
Figure 7: Person B most influential friends on Facebook
Figure 8: Person B degree distribution for most influential friends on Facebook
Table 1: Metrics for Person A and Person B private friends networks
| Graph | Nodes | Edges | Av Degree | Diameter | Av Path Length | Av Clustering | Modularity | Density |
| Person A, All friends | 911 | 4297 | 9.4 | 9 | 3.5 | 0.249 | 0.519 | 0.01 |
| Person A, Most influential friends | 47 | 161 | 6.9 | 6 | 2.5 | 0.354 | 0.351 | 0.149 |
| Person B, All friends | 1015 | 4613 | 9.1 | 11 | 3.5 | 0.318 | 0.444 | 0.009 |
| Person B, Most influential friends | 52 | 178 | 6.8 | 7 | 2.6 | 0.419 | 0.301 | 0.134 |
It’s important to note from the data above that for both individuals their most “influential” friends are more interconnected (lower path length, diameter, higher clustering and lower modularity) than the network in general. However, it’s still far away from being a tightly-knit “clique”, as there is heterogeneity present within the both networks’ structures.
3. MODELING CULTURAL NETWORKS: PAF AND INPEX
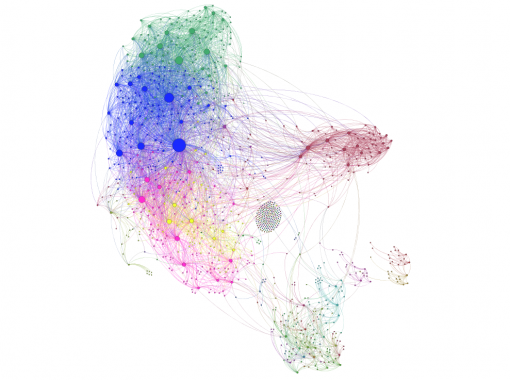
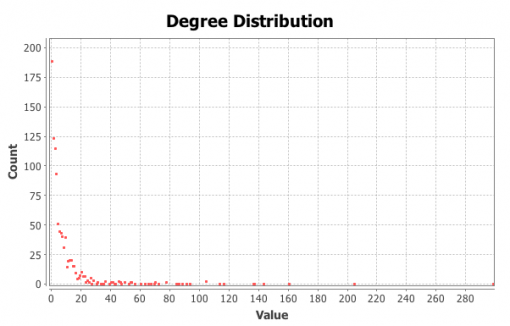
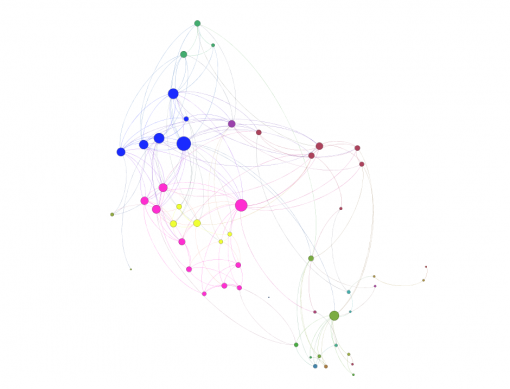
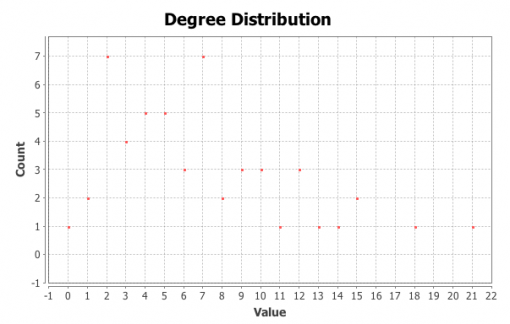
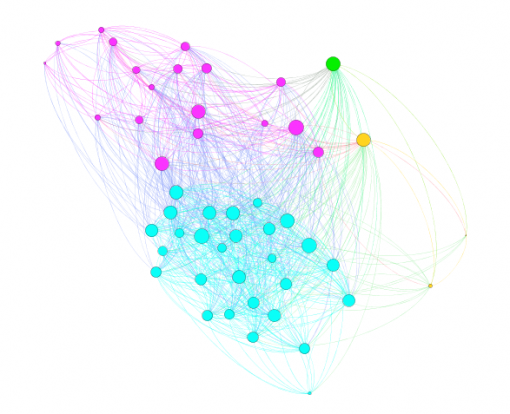
For the next step we will model each individual’s cultural professional networks, PAF and INPEX, following the same procedure described in Chapters 1 and 2 above. We import the data from Facebook, visualize it in Gephi, detect communities of nodes that are more densely connected together than with the rest of the network, increase the size of the nodes that have more connections. Below we can see their visualizations (Figures 9 and 11) along with degree distribution charts (Figures 10 and 12).
Figure 9: PAF – Performing Arts Forum Network
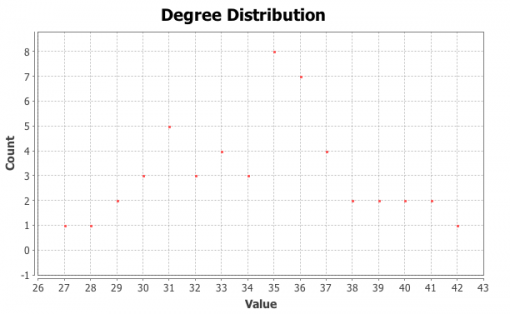
Figure 10: PAF network degree distribution
Figure 12: Degree distribution in INPEX network
We will now filter each individual’s “ego network” to include only the nodes that the study subjects are connected to directly in their respective networks. This will allow us to see the topological differences between the subjects’ immediate surrounding within the professional groups they belong to and the groups at large. This is a necessary step in analysis because it allows us to gain a more subjective view on a professional network, from the point of view of the individual who belongs to it. We can then talk about a network not as some kind of abstract entity, but as a group of people that our study subjects have direct influence on (which will become important later in our discussion of possible strategies that individuals can take within the network in order to maintain its innovation potential in a sustainable way).
Figure 13: PAF network, neighbors of Person A only
Figure 14: Degree distribution among Person A’s neighbors within PAF network
Figure 15: INPEX network, neighbors of Person B only
Figure 16: Degree distribution among Person B’s neighbors within INPEX network
Table 2: Metrics for PAF and INPEX networks
| Graph | Nodes | Edges | Av Degree | Diameter | Av Path Length | Av Clustering | Modularity | Density |
| PAF Network | 723 | 8129 | 22.5 | 7 | 2.7 | 0.395 | 0.33 | 0.031 |
| Person A neighbors at PAF net | 69 | 711 | 20.6 | 4 | 1.7 | 0.581 | 0 | 0.303 |
| Person A neighbors at PAF net, 5% most influential (in total net) | 39 | 397 | 20.4 | 2 | 1.5 | 0.722 | 0 | 0.536 |
| INPEX Network | 919 | 15128 | 32.9 | 6 | 2.5 | 0.459 | 0.39 | 0.036 |
| Person B neighbors at INPEX net | 162 | 3344 | 41.3 | 4 | 1.8 | 0.638 | 0.21 | 0.256 |
| Person B neighbors at INPEX net, 5% most influential (in total net) | 50 | 814 | 32.6 | 3 | 1.3 | 0.8 | 0 | 0.664 |
It can be seen from Figures 9 and 11 that there are 3 large communities within both of these networks (Blondel 2008). The degree distribution chart for both PAF and INPEX networks (Figures 10 and 12) follows exponential distribution, so both networks are scale-free (Newman et al 2006): there’s a few, but significant number of nodes that have many connections, but most of the nodes have only a few. However, both PAF and INPEX networks have higher clustering than social networks and are much more densely connected (Table 2).
Moreover, if we filter both networks and include only the nodes that the study subjects have direct connection with (“ego networks” within each professional network), we will see (Figures 13 and 15 and Table 2) that both clustering, density, and overall connectivity increases even more. Clearly, the direct contact network of each study subject within their professional surrounding is much more densely connected than their friends network and has less defined community structure as the modularity measure decreases (Blondel 2008). It can also be seen that both study subjects are well integrated within the existing communities in their professional networks.
The degree distribution for Person’s A ego network who are also part of PAF network is, however, different from the whole network (compare Figure 14 and Figure 10). It’s closer to a bell curve than exponent, following Poisson (normal) distribution, which is more typical for random graphs (Newman et al 2001). This is an important difference (along with the higher clustering) of the individual’s professional network from their private network, which we will address later.
The situation is Person’s B ego network is a bit different. The degree distribution is somewhat between Poisson and exponential distribution, but both clustering and density of connections are much higher than for INPEX network in general (similar results as Person’s A PAF network).
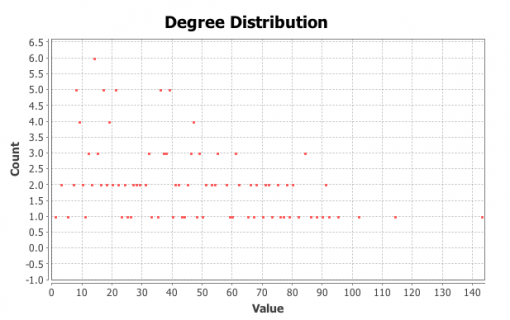
Our next step will be to include only those nodes, for both individuals, that exert the most influence in their respective networks. So we will filter their ego network even further to include only the nodes, which have the highest betweenness centrality in the overall network (Freeman 1977; Brandes 2001). This will give a more realistic image of the both individuals’ interactions within their respective network, as it will include only the nodes that participate more often in information dissemination within the network. We will refer to this group of the most influential individuals in our study subjects’ ego networks as “influencers” further on.
Figure 17: PAF network, the most influential neighbors of Person A
Figure 18: PAF network, degree distribution for the most influential neighbors of Person A
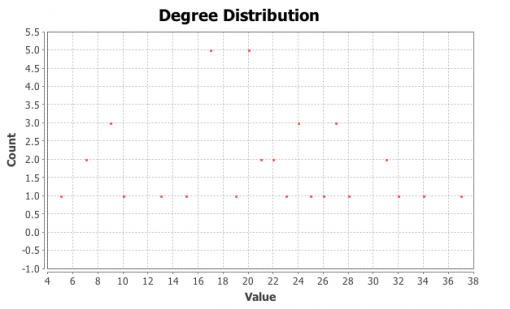
Figure 19: INPEX network, the most influential neighbors of Person B:
Figure 20: Degree distribution for the most influential neighbors of Person B in INPEX
It can be clearly seen (Figure 18 and 20) that the degree distribution in these both “influencers” networks is now Poissonian, following a bell curve. Thus, both graphs are even closer to random graph topology.
It can also be seen (Table 2) that the clustering and graph density increased even more for both networks as we filtered each individual’s neighbors and left only the most influential ones. This raise in the clustering and density measures – as we left only the most influential members – was much steeper for professional networks than in the subjects’ friends networks.
4. DISCUSSION: PRIVATE FRIENDS NETWORKS VS PROFESSIONAL CULTURAL NETWORKS
We will now proceed to the discussion of structural, topological and quantitive differences between the study subjects’ private friends networks and their professional cultural networks.
First, if we compare both the individuals’ private and professional networks we will see that while the both are scale-free (their degree following exponential distribution), the professional networks seem to be much more densely connected and have a higher modularity measure (compare Tables 1 and 2), indicating the presence of more distinctively different communities (Blondel 2008). This is also confirmed through the graphs (compare Figures 1 and 3 to Figures 9 and 11), which were created using Force-Atlas layout (Jacomy 2009) derived from force-layout algorithm for graph clustering (Noack 2007). This algorithm pushes the most connected nodes (hubs) away from each other, while aligning the nodes that are connected to the hubs in clusters around them.
This could be explained by the fact that individuals in everyday life may be more willing to be connected to various distinct (often separated) communities (family, former school, work, hobby), while their professional networks have less pronounced community structure and tend to bring different people and communities together around specific agenda, interests, principles, or goals.
However, it’s important to narrow down the scope of our inquiry by limiting the data we use to talk about cultural networks. If we look at a professional network as a whole, from a “bird’s eye view”, we see scale-free structure. However, when an individual is part of such network they tend to interact with their immediate neighbors. So if we are to compare our study subjects’ private friends network (people they personally know in their social circle) to their professional network, we have to limit the individuals we analyze in their professional network to those they can interact with personally. This way we will be looking at a professional cultural network from the point of view of our study subject, which is a better choice methodologically if we are to compare the properties of this network to our study subject’s private friends network.
Therefore if we filter out the nodes and show each individual’s “ego network” within their professional network (members of the cultural network they have direct access to), we will see that these are extremely more connected and have much higher density than the individuals’ private friends network (compare Tables 1 and 2 and Figures 13 and 15 to Figures 1 and 3). The graph density is 20 to 30 times higher, the average degree (the number of connections each person has) is 2 to 4 times higher than in their private friends networks. This confirms that fact that professional cultural networks tend to be much more interconnected than real-life social friends networks and that community structure is much less pronounced in them.
Moreover, for both “ego networks” (Figure 13 and 15), the degree distribution shifts closer to a bell curve than exponent, following Poisson (normal) distribution, which is more typical for random graphs (Newman et al 2001).
Finally, if we further filter the network and leave the most influential nodes that are responsible for conducing the most information within the individuals’ immediate surrounding in their respective professional cultural networks we will see (Figures 17, 18, 19, and 20) that they move even closer topologically to random graphs. Degree distribution is now following Poissonian curve and most of the most influential nodes have the average (high) number of connections. This is very different to the graphs we obtained through filtering out the most influential members in our study subjects’ private friends networks (Figures 5, 6, 7 and 9] where degree distribution still followed exponential curve and only a few most influential members also had many connections within this filtered network. This shows that groups of “influencers” in our study subjects’ professional cultural networks tend to be more densely connected together than the most influential individuals in their private friends networks. A possible explanation is that when a community structure is much more pronounced (scale-free network), individuals tend to reach out much further from their vicinity than they do in professional cultural networks. In everyday life we tend to connect to people who are well-connected within their own distinct communities and these most connected people do not necessarily have to all know each other.
It’s important to address the fact that the “ego networks” within our study subjects’ professional cultural networks and especially the smaller “influencers” group networks were topologically very close to random graphs with Poissonian degree distribution versus exponential (scale-free) distribution in private friends networks.
In fact, if we generate a random graph with Poissonian distribution (Erdos & Renyi 1960) with 50 nodes and the wiring probability p = 0.7 (Figure 21), we will see (Table 3) that their main parameters (short path length, average degree, diameter, clustering) are very similar, and that the degree distribution also looks very much alike (compare Figure 18.20 and 22).
Figure 21: Random graph, 50 nodes, wiring probability p = 0.7

Table 3: Comparison of a random network to the networks of the most influential members in INPEX and PAF.
| Parameter | Random Network (p=0.7) |
INPEX Most Influential Members | PAF Most Influential Members |
| Average path between the nodes | 1.3 | 1.3 | 1.5 |
| Diameter (longest path) | 3 | 2 | 3 |
| Average degree | 34.5 | 32.6 | 20.4 |
| Clustering coefficient | 0.7 | 0.8 | 0.7 |
Figure 22: Degree distribution chart for a random network
As can be seen (Figures 13, 15, 17, 19) all the graphs we generated for cultural networks and subgroups within them are quite dense: every node is chained to many other nodes, the network is closed onto itself, making it quite hard to enter, leave, or rewire. In this way they are very similar topologically to random graphs (Figure 20).
This is the “dynamique d’enfer” in action, which has its positive sides (innovative potential, ability to act decisively and fast) and negative sides (exclusivity, closure, isolation), as mentioned in the Introduction (Koolhaas 1993 and Spangberg 2011).
To clarify these observations, let’s see what are the different properties of random graphs versus real-world scale-free networks.
First, it has been shown that as the probability of any two random nodes to be connected (or the density) increases in the network, the epidemic threshold decreases (Pastor-Satorras & Vespignani 2001), making them more open to information propagation. That means that highly connected random networks will much more readily accept and follow a certain ideology as a unified whole than scale-free networks, where the existence of communities ensures that there will always be several competing forces in play.
Moreover, as we observed above, the most influential members in cultural networks tend to be much more densely connected together than the most influential members in private social friends network. The degree distribution of such densely interconnected clusters of the most influential members in cultural networks follows Poisson distribution (close to that of a random graph). This makes such groups very efficient in picking up on a trend or piece of information and then spreading it to the rest of the network.
It has been shown that when the number of connections in random networks increase, the oscillations in their infection rates also increase (Abramson & Kuperman 2001) due to the higher rate of node synchronization in less orderly networks. In other words, contagions can take over larger populations much quicker in such networks than in the more ordered scale-free friends networks.
This is a confirmation of the fact that the cultural networks (and especially the densely connected cliques of the most influential members) are much more likely to pick up on a certain trend, gossip, or a piece of information and spread it further to a larger population. The oscillations of trends are much stronger in cultural networks (especially in the “influencers” cliques) and they are much more susceptible to a sudden change of direction. While this can be a positive trait for innovative networks in the short-term (Dhanaraj 2008; Tsai 2001), it’s very arguable whether such malleability is beneficial in the long-term, especially when it’s necessary to be consistent or to sustain a certain operation or commitment for a longer time.
To clarify this last point, we should note once again that random networks tend to shift towards high amplitude oscillations when the number of connections increases (when probability of two nodes connected p > 0.5), which makes the behavior of such networks quite unstable and unpredictable (Abramson & Kuperman 2001). Therefore, while random networks have innovative potential, they are not really sustainable in long-term and also can even be dangerous in the way that an uncontrolled unified mass can be. In Hanna Arendt’s words: “Totalitarian movements are possible wherever there are masses who for one reason or another have acquired the appetite for political organization.” (Arent 1951)
In other words, if a network with random graph topology (Poisson distribution of node degrees) reaches a point where most of the nodes have many connections (p > 0.5), effaces most differences, and establishes a certain internal hierarchical structure, it becomes very easy to pour any ideology into that structure and be more or less confident that it would readily be taken on by the network for further dissemination. High connectivity makes it also much less likely for nodes to make new connections or to rewire the network, especially for the most influential nodes.
To summarize, random networks have a higher capacity to mobilize, follow a trend, and disseminate information. At the same time, nodes in random networks connect to each other, exchange, and cooperate in an almost promiscuous manner compared to the nodes in scale-free networks (higher connectivity and density of connections leads to more possibilities for information dissemination). In this way, random network structure seems to be optimal for knowledge diffusion and mobility (Gilbert et al 2001), as well as innovation appropriability (Dhanaraj 2008) and innovation (Koolhaas 1993). However, we’ve also shown that the most influential nodes in random networks tend to be much more connected to each other than to the periphery. This makes it very hard for some nodes or communities who have important knowledge resources to take the much-needed central position within the network (Tsai 2001). This also makes it harder to maintain a combination of strong and weak ties that is important for innovative networks (Capaldo 2006), leading to exclusivity and isolation (Spangberg 2011). This hermetic property of professional cultural networks (especially vivid at their core) also hinders so-called “creative reactions” important for maintaining innovative potential within the network (Antonelli et al 2011), which depend on the node’s ability to access knowledge beyond their immediate vicinity.
Another important feature of random networks with Poisson distribution of degree is that they are known to be more susceptible to random node removal than scale-free networks (Albert et al 2000). This explains the fact why “dynamique d’enfer” is so important in cultural networks: when the cost of connections is not very high, it’s very easy to leave, and when a few members leave the network it is much more likely to disintegrate than scale-free network. Therefore higher exclusivity and symbolic barriers to entry may be a mechanism employed by cultural networks to compensate susceptibility that arises due to their random graph topology. It has been shown that groups with the high cost of entry and simultaneous presence of highly charismatic leaders tend to achieve long-term stability (Wildman & Sosis 2011). This latter finding could explain the necessity of a strong personality cult in cultural (Spangberg 2011) and innovative (e.g. Apple) networks (Kahney 2008) as a way to compensate for their instability in comparison to scale-free (friends) network. It’s also interesting to note that the clique of the most influential members in the INPEX network seem to have a much more densely connected, exclusive, and closed structure than the PAF network. This observation coupled with the fact that Marten Spangberg himself is the founder and the most connected member of INPEX network makes us consider the possibility that his rant (Spangberg 2011) about the exclusivity of cultural networks was partially addressed to himself.
In everyday life our study subjects’ friends networks are scale-free, which is the case for most real-life networks (Newman et al 2006). That means that a few, but significant number of hubs accumulate most of the connections while the other nodes get the status of the periphery. The nodes form communities around hubs, the network operates on the basis of differences between the participants. These properties typical for scale-free networks make them more open and inclusive than random (and cultural) networks. It’s very easy to join, there is no one leader, one can belong to several communities at once. Once a node is integrated, it can become a hub by forming links with the other outsiders, while connecting to the major hubs to ensure its connectivity to the rest of the network.
5. CONCLUSION
We have shown above that the professional cultural networks we studied had certain advantages and disadvantages resulting from their topology, which was close to random graph structure. It’s important to notice that we analyzed these cultural networks from the point of view of specific individuals who belonged to them, allowing us to be able to compare these individuals’ private friends networks to their professional cultural networks.
The advantages of the professional cultural network structure (comparing to the friends network) were its higher potential for knowledge dissemination, synchronized mobilization, and trend propagation. The disadvantages were its lesser stability, higher susceptibility to attack, and disposition to higher rates of fluctuation, which were compensated by a high cost of entry, exclusivity, and the need to have strong leadership. These “symptoms” were shown to be a hindrance to building innovative networks, therefore potentially undermining the advantages that these networks had because of their close to random graph topology. We’ve also shown that random networks have a higher capacity to turn into an uncontrolled “mass”, transforming into an authoritarian homogenous structure and thus stifling its innovative potential even further.
Therefore it would be interesting for us to discuss what would be a way to bring together the openness and stability inherent in scale-free networks while retaining the innovative potential of random networks. This is especially important for cultural networks, which strive on innovation and have to operate on a very limited budget. We will discuss the possible strategies below.
One possibility can come from any individual within the cultural network, who transcends the densely interconnected structure and reaches for the new frontiers. A shot into the unknown, refusal to obey, a fanatical gesture breaking through the dense web and going for the winning throw into the random void, which was actually proposed by Marten Spangberg later in his work that we quoted above (Spangberg 2011) and which is the plot of Tarkovsky’s Stalker film (Tarkovsky 1979). Such strategy is also exemplified by the reactionary movements, which base their ideology on denying whatever it is that is dominant. Popular uprisings function on this basis: from Russian revolution (Trotsky & Eastman 1932) to Occupy Wall Street movement (Korten 2011). Leaving the network in order to evolve. However, in cultural networks, and any closely knit structures, such gesture can only be expected on mass-scale from those at the periphery, who don’t have much to lose. If enough nodes defect from a random network, it will collapse, because its connectivity will be severely affected. So the problem here is that this strategy might work for an individual, but is unlikely to have an effect on the whole group, unless it’s a mass betrayal. Another problem is that in the latter case the structure that’s formed from those isolated individuals who defected is not guaranteed to avoid similar deficiencies and might in fact lead to the formation of totalitarian foam-like mass (Arendt 1951; Trotsky & Eastman 1932; Sloterdijk 2004).
Another strategy is to put a time limit to the existence of a random network. When the network reaches the point of high connectivity and is starting to produce change as a unified whole, it is shut down, so that the individuals inside are forced to start making connections on the outside of the network. For example, temporary projects, artist residencies (Silverstein 2005), project groups, and agile development practices in software development (Shore & Warden 2008) are often based on this approach. The problem here is that the potential of the network is only utilized for a short period of time as it’s only temporary.
Finally – and that is, in our opinion, the most efficient approach – is for a cultural network to dynamically maintain a certain level of connectivity and random structure that allows it to be easily mobilized and innovative without making it too exclusive, unstable, or hermetic.
It has been mentioned before that as probability of nodes’ connectivity increases, random networks tend to shift to high amplitude of oscillations (Abramson & Kuperman 2001) and thus become less stable. At the same time, there’s a certain level of connectivity required in random networks in order for bi-fan and feedback loop motifs to emerge within them (Milo et al, 2002) thus making them more conducive to information dissemination. We could say, then, that there should be dynamic process active in cultural networks, which keeps its connectivity at a certain level that allows it to utilize its potential for information dissemination while keeping it stable and open at the same time.
We have some suggestions as to how this range of connectivity could be maintained and they also indicate the future direction of our research.
First, the network as a whole should be always on the lookout for the other networks (based on the similar “dynamique d’enfer” principle) and the individual nodes should be willing to forge the connections to the nodes from other networks. The inclusion should happen as globally as possible to avoid the formation of hubs, but at the same time there should be a degree of hesitation or exclusivity in order to avoid the formation of a “mass”. This will allow these networks to combine their innovative potentials without compromising the equality and ease of communication within each network (Figure 23).
Figure 23: Two random networks merging
Second, the network should avoid being too hermetic. If it’s too locked on itself then at some point it will reach a gridlock, become a “mass”, lose its specificity. It should be always on the lookout for the new elements from the outside and make new connections with them, integrating them into the network. In order to ensure that they don’t bring with them a dominating power structure these elements can be taken from the “foam”: a free floating mass of nodes or small communities, which do not belong to certain groups or organizations, but are ready to join (even temporarily) to a structure whose purposes they share. At the same time as this inclusive movement is happening it should be combined with the exclusive movement on the part of those nodes inside the network who are willing to “travel” towards other formations. Otherwise, this constant inclusion will simply maintain the existing hierarchies and increase the size of the network, which may be not sustainable in long term. The inclusive movement should happen on the periphery, while the exclusion should happen from the center towards the periphery to allow for the constant renewal and sustainability (Figure 24). The nodes from the periphery will take central positions and the central nodes will become periphery.
Figure 24: A random network and “foam” merging
In a way, this latter strategy is related to the previous proposition to form temporary random networks, because there will be a certain time limit on how long a node can be part of the main component. Rotating boards in cultural organizations are a good example.
Thus, our proposition for the dynamic process of forging new links and breaking the old ones is akin to limit-cycle behavior exhibited by what is called “dissipative structures” (Prigogine 1980), which settle down into periodic patterns and produce non-equilibrium stability. The resulting network functions on the basis of constant interplay between inclusivity and exclusivity. The clusters on the periphery are inclusive towards the “foam”, forming communities based on random distribution of power. Constant influx of newcomers will ensure the maintenance of differences within the community that allow for individuation and makes the community exclusive. The nodes that cannot identify with a community will make random shots into the unknown, becoming a foam, only to be integrated at some later point of time again. The communities, as soon as they reach a point of a unified whole, will align together to foster new connections and the same process will happen on a meta scale, forming super-networks comprised of the already existing ones.
Inclusive exclusivity of “dynamique d’enfer” in action.
“Decisive here is the idea of an inessential commonality, a solidarity that in no way concerns an essence. Taking-place, the communication of singularities in the attribute of extension, does not unite them in essence, but scatters them in existence.” (Agamben 1993)
Figure 25: A snapshot of Belousov-Zhabotinsky reaction (source: http://www.flickr.com/photos/hawkexpress/3742135730/ )
RESOURCES
ABRAMSON, G.; KUPERMAN, M. (2001). Small World Effect in an Epidemiological Model. In Physical Review Letters, 86-13
ADAR, E. (2006). GUESS: A Language and Interface for Graph Exploration. In CHI ’06 Proceedings of the SIGCHI conference on Human Factors in computing systems: 791-800
AGAMBEN, G. (1993). The Coming Community. University of Minnesota Press
ALBERT, A., JEONG, J., BARABASI, A.L.; (2000). Error and Attack Tolerance of Complex Networks. In Letters to Nature, 406: 378-382
ANTONELLI, C; FERRARIS, G. (2011). Innovation as an Emerging System Property: An Agent Based Simulation Model. In Journal of Artificial Societies and Social Simulation 14 (2)
ARENDT, H. (1951). The Origins of Totalitarianism
BASTIAN, M.; HEYMANN, S.; JACOMY, M.; (2009). Gephi: An Open Source Software for Exploring and Manipulating Networks. Association for the Advancement of Artificial Intelligence
BLONDEL, V.; GUILLAUME, J-L; LAMBIOTTE, R; LEFEBRE, E; (2008). Fast Unfolding of Communities in Large Networks. In Journal of Statistical Mechanics: Theory and Experiment, Volume 2008
BRANDES, A. (2001). Faster Algorithm for Betweenness Centrality. In Journal of Mathematical Sociology 25(2):163-177
CAPALDO, A. (2006). Network Structure and Innovation: The Leverating of a Dual Network as a Distinctive Relational Capability. In Strategic Management Journal, 28, 585-608
DHANARAJ, C.; PARKHE, A; (2008). Orchestrating Innovation Networks. In Academy of Management Review 2006, Vol. 31, No. 3, 659–669.
GEPHI. Graph visualization, manipulation and analysis software. URL: http://www.gephi.org
GILBERT, N.; PYKA, A.; AHRWEILER, P; (2001). Innovation Networks – A Simulation Approach. In Journal of Artificial Societies and Social Simulation 4 (3)
ERDOS, P; RENYI, A; (1960). On the Evolution of Random Graphs. Institute of Mathematics, Hungarian Academy of Science.
FACEBOOK. Online social network. URL: http://www.facebook.com
FREEMAN, L. (1977). A Set of Measures of Centrality Based on Betweenness. Sociometry Vol. 40, No. 1 (Mar., 1977): 35-41
INPEX. The Swedish non-profit organization. URL: http://www.inpex-universe.org
JACOMY, M. (2009). Force-Atlas Graph Layout Algorithm. URL: http://gephi.org/2011/forceatlas2-the-new-version-of-our-home-brew-layout/
KAHNEY, L (2007). Inside Steve’s Brain. New York: Portfolio Hardcover
KOOLHAAS, R. (1993). Beyond Delirious. From the lecture at University of Toronto School of Architecture
KORTEN, D. (2011). From Wall Street to Main Street: Capitalism and the Common Good. Lecture at The Wayne Morse Center for Law and Politics: 2011-2013 Inquiry
MILO, R; SHEN-ORR, S.; ITZKOVITZ, S; KASHTAN, N; CHKLOVSKII, D; ATON, U. (2002). Network Motifs: Simple Building Blocks of Complex Networks. In Science, 298
NETVIZZ. Facebook application for graph data retrieval. URL: http://apps.facebook.com/netvizz/
NEWMAN, M.; STROGATZ, S.H.; WATTS, D.J.; (2001). Random Graphs with Arbitrary Degree Distributions and Their Applications. In Physical Review E, Vol 64, 2
NEWMAN, M., BARABASI, A., WATTS, D.J., (2006). The Structure and Dynamics of Networks. Princeton University Press
NOACK, A. (2007). Energy Models for Graph Clustering. In Journal of Graph Algorithms and Applications, vol 11, no 2: 453-480
PAF. Performing arts forum. URL: http://www.pa-f.net
PASTOR-SATORRAS, R.; VESPIGNANI, A; (2001). Epidemic Spread in Scale-Free Networks. In Physical Review Letters 86-14, 2001
PRIGOGINE, I. (1980). From Being to Becoming. WH Freeman
SHORE, J & WARDEN, S. (2008). The Art of Agile Development. O’Reilly
SILVERSTEIN, L. (2005). Artist Residencies: Evolving Educational Experiences. In Acts of Achievents: The Role of Performing Arts in Education
SLOTERDIJK, P. (2004). Sphären III – Schäume. Suhrkamp
SPANGBERG, M. (2011). Spangbergianism. Stockholm: INPEX
TARKOVSKY, A. (1979). The Stalker. Moscow: Mosfilm
THE ECONOMIST (2007). Lessons from Apple. The Economist Newspaper Limited, printed edition Jun 7, 2007
TROTSKY, L; EASTMAN, M. (1932). The History of Russian Revolution. URL: http://www.marxists.org/archive/trotsky/1930/hrr/index.htm
TSAI, W. (2001). Knowledge Transfer in Intraorganizational Networks: Effects of Network Position and Absorptive Capacity on Business Units Innovation and Performance. In Academy of Management Journal, 2001. Vol. 44. No. 5, 956-1004.
WILDMAN, W & SOSIS, L; (2011). Stability of Groups with Costly Beliefs and Practices. In Journal of Artificial Societies and Social Simulation 14 (3) 6
YOO, Y; LYYTINEN, K; BOLAND, R; (2008). Distributed Innovation in Classes of Networks. Proceedings of the 41st Hawaii International Conference on System Sciences